Double Distance aim for Ghost Ball
- Thread starter LAMas
- Start date
LAMas:
The only problem I see with the "double-the-distance" ghostball aiming method, is that some folks might confuse this with the "aim with the side of the cue" or "aim with the side of the ferrule" method. In other words, you know that yellow line you show in your [great] diagram? Lots of folks will extend that line all that way back to the cue tip, and line it up with the very edge of the cue shaft/ferrule itself. This is very, very wrong.
If one has an Earl Strickland-esque extended pro taper on their shaft that goes as close to the joint as possible, this technique *might* work, for a time and for certain shots. But the following problem exist:
1. Some folks, like me, prefer a standard/non-tapered shaft (commonly referred to as a "standard conical taper") -- just as is popular in Europe, and is popular on your standard Wall-abushka (house cue). Obviously, using the very edge/side of the cue is completely incorrect, and will cause you to undercut many shots.
2. Even with an extended pro taper which tends to keep the shaft the same diameter as far up the shaft as possible, lining up the edge of the shaft is still incorrect, especially as the cut gets thinner and thinner (because the distance you're doubling is greater than the radius or diameter of the shaft).
Double-the-distance is geometrically correct only when dealing with the very center of the cue ball and object ball.
Hope this is helpful -- comments?
-Sean
The only problem I see with the "double-the-distance" ghostball aiming method, is that some folks might confuse this with the "aim with the side of the cue" or "aim with the side of the ferrule" method. In other words, you know that yellow line you show in your [great] diagram? Lots of folks will extend that line all that way back to the cue tip, and line it up with the very edge of the cue shaft/ferrule itself. This is very, very wrong.
If one has an Earl Strickland-esque extended pro taper on their shaft that goes as close to the joint as possible, this technique *might* work, for a time and for certain shots. But the following problem exist:
1. Some folks, like me, prefer a standard/non-tapered shaft (commonly referred to as a "standard conical taper") -- just as is popular in Europe, and is popular on your standard Wall-abushka (house cue). Obviously, using the very edge/side of the cue is completely incorrect, and will cause you to undercut many shots.
2. Even with an extended pro taper which tends to keep the shaft the same diameter as far up the shaft as possible, lining up the edge of the shaft is still incorrect, especially as the cut gets thinner and thinner (because the distance you're doubling is greater than the radius or diameter of the shaft).
Double-the-distance is geometrically correct only when dealing with the very center of the cue ball and object ball.
Hope this is helpful -- comments?
-Sean
I withdraw my question
Last edited:
Yes your comments are helpful.
I aim the center of the CB to the spot that is double distance from the contact point.
The colored photo pic is taken from another thread and is not mine, but it shows that the CP on the OB is parallel to the actual double distance spot.
I tried aiming down the side of the cue shaft, I use a Z2 which is not conical, but I suffer from parallax confusion and when the cut is 90 degrees (thin), the shaft needs to be a larger diameter etc.:smile:
The big problem is to find the DD spots that are off of the OB (30-90 degrees) and on the felt or rail, also the spots for 75 degrees to 90 degrees are very close together...ergo, I sometimes miss.:smile:
If one can memorize the spots and visualize them, when down - it is as, you know, a direct method of aiming
Thanks.
Last edited:
peteypooldude:
As long as there's no snide comments or "prairie justice" for what's going on in the CTE threads (which I'm so sorry to see the degeneration of), there is no dumb question here.
I did briefly see your question, and wanted to respond to it (methinks it had to do with my point on side-of-shaft/side-of-ferrule aiming?), but work issues pulled me away.
Any particular reason you retracted the question?
-Sean
************
If one can memorize the spots and visualize them, when down - it is as, you know, a direct method of aiming
Thanks.
**********************
I am not exactly sure what it is you are looking for.
As has been posted in this forum before, the aim point on the OB is approximately 1 mm off center for every degree of cut for the range 0-30 degrees. Beyond that, an estimate of 0.8 mm per degree of cut suffices. Therefore, if you can estimate cut angles (also previously discussed in detail), and can estimate mm distances, you know the aim point.
For some, like myself, this approach to fractional ball aiming works very well. But you have to know how to estimate angles to within a degree and off-center distances to within a mm, and this is not the ticket for very many players.
Where are you trying to go with this?
If one can memorize the spots and visualize them, when down - it is as, you know, a direct method of aiming
Thanks.
**********************
I am not exactly sure what it is you are looking for.
As has been posted in this forum before, the aim point on the OB is approximately 1 mm off center for every degree of cut for the range 0-30 degrees. Beyond that, an estimate of 0.8 mm per degree of cut suffices. Therefore, if you can estimate cut angles (also previously discussed in detail), and can estimate mm distances, you know the aim point.
For some, like myself, this approach to fractional ball aiming works very well. But you have to know how to estimate angles to within a degree and off-center distances to within a mm, and this is not the ticket for very many players.
Where are you trying to go with this?
Where am I going with this?
I am only restating the obvious in picture form for aiming spots for every 15 degrees of cut angles that go to the pocket. From these points, one can make adjustments toward the center of the OB if the angle is up to 7 degrees less and toward the outside if the angle is more than 7 degrees,
The example system that you posted is vague – to me.
I find it difficult to see in increments of 1mm at an OB that decreases in diameter as it is moved further away from my eye and the 1mm becomes decreasingly less than 1mm. I think in terms of inches - so 1mm is .03937”
There are 30 degrees included in a straight in shot to a ½ ball shot – 1.125” is ½ of a 2,25” diameter OB. 1.125" divided by 30 degrees = 0375” or very close to 1mm (.03937”)/degree.
There are another 60 degrees from there (30 degrees) to a 90 degree cut that lie within another ½ ball (away from the first or the outer edge of the OB) so 1.125” divided by 60 degrees = .0188” or close to ½mm/degree. Your example says 0.8mm for each degree. This approximation will not be a reliable metric - for me.
Last edited:
A question, I guess. Precisely how do you define the distances?
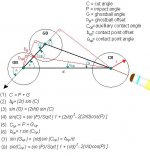
The double-the-distance system has a slight inaccuracy or ambiguity. If you draw out a diagram with the four important points -- the centers of the CB, the OB and the ghost ball, and the contact point -- you will see that the two angles OB-CB-CP and GB-CB-CP are not quite equal. This is more obvious the closer the CB is to the OB. Many players take equal angles to be equal distances in situations like this.
For longer shots, the discrepancy is smaller than other sources of uncertainty.
Here's a definition that removes the ambiguity (that will be interesting only to geometrians): If you drop a perpendicular from the OB to the CB-GB line extended, the CB-CP line will intersect that perpendicular at its midpoint.
Last edited:
Posters here that are in search of methods that can improve their aiming are not particularly interested in geometry or trig....I have been told and I also found out.
You of course are correct that "double distance" is a misnomer and only works when the OB and CB are not "too" close together. The appearance of the center of the OB to the CP being "doubled" at distance is a shortcut to avoid the math.
That the term "double the distance" has been used since before I was born and math applied - attest to that practicality.
Here is the proof of the fallacy provided to me by Jal where bg is not equal to bcp when measured perpendicular to the aim line.
Thanks for your sage input to my small audience.
*****************
There are another 60 degrees from there (30 degrees) to a 90 degree cut that lie within another ½ ball (away from the first or the outer edge of the OB) so 1.125” divided by 60 degrees = .0188” or close to ½mm/degree. Your example says 0.8mm for each degree. This approximation will not be a reliable metric - for me.
**********************
Using the diagram you posted from JAL, I think that we can agree that
bg= 2R* sin(c) over the entire range of cut angles
If you plug in the numbers for 20, 40, and 55 degree cuts, the respective values for bg are:
19.54mm, 36.7 mm, and 46.8 mm.
For the 20 degree cut, my method of estimation is about as good as it gets.
For the two examples beyond 30 degrees:
40 degree cut:
36.7 mm is approximately equal to R + (0.8 * (40-30)), (which works out to 36.6). Not too shabby.
55 degree cut:
46.8 mm is approximately equal to R + (0.8) * (55-30)), (which works out to 48.6)
So, there is some breakdown above 50 degrees, but as a banks player, I not really looking for 55 degree cuts anyway. Therefore, I contend that my method of calculating the aim point is not flawed in the way that you have presented it to be.
I spent quite a bit of time on the double the distance approach, and ultimately found it to be unsatisfactory for a variety of reasons, I hope you have better luck with it.
There are another 60 degrees from there (30 degrees) to a 90 degree cut that lie within another ½ ball (away from the first or the outer edge of the OB) so 1.125” divided by 60 degrees = .0188” or close to ½mm/degree. Your example says 0.8mm for each degree. This approximation will not be a reliable metric - for me.
**********************
Using the diagram you posted from JAL, I think that we can agree that
bg= 2R* sin(c) over the entire range of cut angles
If you plug in the numbers for 20, 40, and 55 degree cuts, the respective values for bg are:
19.54mm, 36.7 mm, and 46.8 mm.
For the 20 degree cut, my method of estimation is about as good as it gets.
For the two examples beyond 30 degrees:
40 degree cut:
36.7 mm is approximately equal to R + (0.8 * (40-30)), (which works out to 36.6). Not too shabby.
55 degree cut:
46.8 mm is approximately equal to R + (0.8) * (55-30)), (which works out to 48.6)
So, there is some breakdown above 50 degrees, but as a banks player, I not really looking for 55 degree cuts anyway. Therefore, I contend that my method of calculating the aim point is not flawed in the way that you have presented it to be.
I spent quite a bit of time on the double the distance approach, and ultimately found it to be unsatisfactory for a variety of reasons, I hope you have better luck with it.
I concur.
I misinterpreted what the poster that you quoted said and what you wrote:
"As has been posted in this forum before, the aim point on the OB is approximately 1 mm off center for every degree of cut for the range 0-30 degrees. Beyond that, an estimate of 0.8 mm per degree of cut suffices."
I assumed that he meant all angles above 30 degrees from 31 degrees to 90 degrees.
Whatever works for you.
Thanks for your input.
I misinterpreted what the poster that you quoted said and what you wrote:
"As has been posted in this forum before, the aim point on the OB is approximately 1 mm off center for every degree of cut for the range 0-30 degrees. Beyond that, an estimate of 0.8 mm per degree of cut suffices."
I assumed that he meant all angles above 30 degrees from 31 degrees to 90 degrees.
Whatever works for you.
Thanks for your input.