Ignore Bait: Highest IQ, Many Questions, Odds makers invited...

[vapoolplayer]

You're hung up on something that doesn't matter. Choice or no choice he will always eliminate a goat and leave a car and a goat. Every time.

If it doesn’t matter, come take my money.

I’m not joking. I’ll bring $500k if you want.

 

[MajorMiscue]

The only way this scenario could be 50/50 is if he turned over the goat, then mixed up the other two cards and you had to pick.

Mixed up doesn't matter. There are two remaining choices, one winner, one loser and monte doesn't get to pick.

 

[MajorMiscue]

66% of the time, the car will be in the card he didn’t turn over and you don’t have in your hand.

And you get to choose again. So that percentage is meaningless.

 

[vapoolplayer]

And you get to choose again. So that percentage is meaningless.

It matters because I know where the car is 66% if the time.

I can literally tell you which of the two doors the car is…..

66 times out of 100

 

[vapoolplayer]

And you get to choose again. So that percentage is meaningless.

The car will be in the door I didn’t choose and he didn’t open…..

Literally 66/100

666/1000

Etc

 

[David in FL]

The odds don’t change - Monty’s two doors are twice as likely to have the prize as your one door, both before and after he shows one of them.

Sorry, Jay, but I’ll take your bet too.

pj
chgo

And that doesn't matter at all. Once a goat is eliminated you are 50/50, regardless of whether you picked the car at first or not.

No. That’s where you’re going wrong, because the second door of the two that you didn’t pick now is twice as likely to have the car as the one that you did pick…

Look at PJ’s post above, and my attempt to explain it below. Maybe that will help.

That is a great way of looking at it.

Let me try…

The answer is because the initial odds were 1 chance vs 2 chances of holding the car for the two sets.

The first set being your choice, and the second set being the other two doors combined.

You always knew going in that the second set might be comprised of one door that had the prize and one that did not.

So, when Monte shows you that one of the doors in the second set doesn’t have the car, it doesn’t change anything, because well, you already knew that. That set still has twice the likelihood of holding the car than the first set does, which means that you now know that the remaining door has twice the likelihood of holding the car…

Did that help?

 

[vapoolplayer]

Mix 3 cards up. Face down.

2, 2, A

Do it 100 times. Pull one to the side. Look at the other two. And turn over a 2 from those two.

I will tell you where the A is out of the last two cards not turned over…..

66 times

 

[MajorMiscue]

If it doesn’t matter, come take my money.

I’m not joking. I’ll bring $500k if you want.

Yes or no, he will leave a goat and a car every time? Y or N.

Yes or no, you always get to choose to stick with your initial choice or switch to the other. Y or N.

Yes or no, in the end there are always two choices one good, one bad and you get to choose. Y or N.

 

[vapoolplayer]

Yes or no, he will leave a goat and a car every time? Y or N.

Yes or no, you always get to choose to stick with your initial choice or switch to the other. Y or N.

Yes or no, in the end there are always two choices one good, one bad and you get to choose. Y or N.

I will be able to tell you where the car is 66% of the time. Y or N??

 

[David in FL]

Yes or no, he will leave a goat and a car every time? Y or N.

Yes or no, you always get to choose to stick with your initial choice or switch to the other. Y or N.

Yes or no, in the end there are always two choices one good, one bad and you get to choose. Y or N.

All yes.

What you’re missing is that one of the choices is twice as likely to be the better one. You‘re mistakingly believing that just because there are two choices, the odds are 50/50. They aren’t.

 

[vapoolplayer]

If I *never* choose the door I picked first…..

I will be correct 66%

 

[vapoolplayer]

All yes.

What you’re missing is that one of the choices is twice as likely to be the better one. You‘re mistakingly believing that just because there are two choices, the odds are 50/50. They aren’t.

I’ve tried explaining this is every way possible.

He’s either a troll or just not smart enough to grasp the concept.

He continually ignores the free money. So, hopefully just trolling.

 

[MajorMiscue]

@David in FL said, "No. That’s where you’re going wrong, because the second door of the two that you didn’t pick now is twice as likely to have the car as the one that you did pick…"

Smoke and mirrors. Monte is always going to have a goat and will always discard the goat leaving a goat and the car and it is your pick, every time. It comes down to 50/50, has to be.

 

[vapoolplayer]

This was fun. But, I’m going to sleep for the day now.

If anyone wants to take me up on the bet, I’ll give 3/2 odds.

If you think it’s 50/50, you can make enough money to retire on.

 

[MajorMiscue]

All yes.

What you’re missing is that one of the choices is twice as likely to be the better one. You‘re mistakingly believing that just because there are two choices, the odds are 50/50. They aren’t.

What you're missing is that it doesn't matter. Monte only gets to choose to throw away a goat, whether he is looking at two goats or a goat and a car. what's left is a goat and a car, every time.

 

[David in FL]

What you're missing is that it doesn't matter. Monte only gets to choose to throw away a goat, whether he is looking at two goats or a goat and a car. what's left is a goat and a car, every time.

Yep. and now the car is twice as likely to be behind the door that wasn’t initially chosen.

It’s just math. We can explain it to you, hell, the entire Internet can explain it to you and has if you bother to look, but we can’t make you understand it. Not for lack of trying though…

 

[straightline]

Absolutely nothing to do with this scenario.

Repeated attempts have everything to do with the odds playing out. I do get that a gambler can play the odds on a one shot because if it loses it's absorbed into a system that's alway on good odds.

 

[MajorMiscue]

I will be able to tell you where the car is 66% of the time. Y or N??

No. Monte will be able to tell me where the car is 100% of the time but he can't do anything to change that. He must discard a goat and leave a goat and the car.

 

[MajorMiscue]

@David in FL answer the questions please:

Yes or no, he will leave a goat and a car every time? Y or N.

Yes or no, you always get to choose to stick with your initial choice or switch to the other. Y or N.

Yes or no, in the end there are always two choices one good, one bad and you get to choose. Y or N.

 

[northdakotafats]

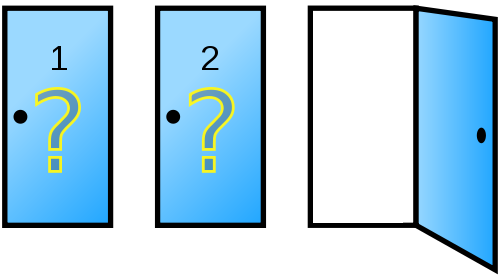
The Monty Hall Problem: A Statistical Illusion

The Monty Hall problem is extremely counter-intuitive because our statistical assumptions are incorrect. I explain how this happens and make sense of it.

statisticsbyjim.com

It isn't that hard to understand when explained correctly.

Very simple. If you switch every time you win every time you pick the wrong door which puts you at 2/3 win rate as opposed to the 1/3 rate of not switching.