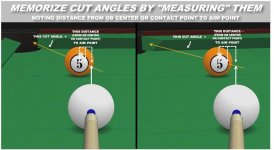
We need another aiming method, right?:smile:
In another thread, an AzB member said that his aiming method, for anything other than very thin or very thick cuts, was essentially to aim 1/2" outside the intended contact point on the object ball. After some discussion, he now realizes that 1/2" is not the correct distance for all such shots, and that the actual distance increases continuously as the cut angle increases.
But that discussion led me to see that we could actually devise a rational aiming method based on some reference distances from the contact point.
Just to be clear, the distance I am talking about for any particular shot is the perpendicular distance from the line of aim (the line through the centers of the CB and the ghost ball) to the contact point at the moment of contact. If you think of the OB as a flat disk with a dot on the horizontal center line for the contact point, then the distance I am talking about is on that same center line of the disk and farther away from the pocket.
This distance is zero for a straight shot -- you aim straight at the contact point, not outside it. This distance is 1 1/8" for a (perhaps theoretical) 90-degree shot -- it's fully half of a ball outside the edge of the OB. For other cut angles, the distance increases continuously, but not linearly, as the cut angle increases. Here are the number of degrees in the cut angle for each eighth of an inch outside the contact point (with no spin and ignoring cut-induced throw):
Turning it around, here are the from-contact-point distances for the cut angles divisible by ten:
OK, this is all well and good, but how can we actually make a usable aiming method out of it? Well, we don't have to use all those distances or be able to recognize all those cut angles. For example, in fractional-ball aiming, or SAM, or back-of-the-ball aiming, we generally use just a small number of reference aims -- 3/4-ball aim (14.5-degree cut), 1/2-ball aim (30-degree cut), 1/4-ball aim (48.6-degree cut) -- and then we use our feel or experience to aim a little thicker or a little thinner for shots between those reference points. So let's do something similar with distance-from-contact-point aiming.
We could, for example, use quarters of an inch from the contact point for our references:
Now, I fully appreciate that this method has some shortcomings that would make it undesirable for many (probably, most) people. It relies on identifying the contact point and then keeping that "in sight" long enough to identify another point a certain distance away from it -- and then keeping that new "invisible" point in sight as an aiming target. That is all complicated by the fact that any particular distance from the contact point appears smaller as the distance to the OB increases.
While this method will not be replacing my own current way of aiming, I thought it would be interesting to some people at least from an academic standpoint. And I wouldn't be surprised if it was actually helpful to someone as a real aiming method.
In another thread, an AzB member said that his aiming method, for anything other than very thin or very thick cuts, was essentially to aim 1/2" outside the intended contact point on the object ball. After some discussion, he now realizes that 1/2" is not the correct distance for all such shots, and that the actual distance increases continuously as the cut angle increases.
But that discussion led me to see that we could actually devise a rational aiming method based on some reference distances from the contact point.
Just to be clear, the distance I am talking about for any particular shot is the perpendicular distance from the line of aim (the line through the centers of the CB and the ghost ball) to the contact point at the moment of contact. If you think of the OB as a flat disk with a dot on the horizontal center line for the contact point, then the distance I am talking about is on that same center line of the disk and farther away from the pocket.
This distance is zero for a straight shot -- you aim straight at the contact point, not outside it. This distance is 1 1/8" for a (perhaps theoretical) 90-degree shot -- it's fully half of a ball outside the edge of the OB. For other cut angles, the distance increases continuously, but not linearly, as the cut angle increases. Here are the number of degrees in the cut angle for each eighth of an inch outside the contact point (with no spin and ignoring cut-induced throw):
1/8" = 6.4 degrees
1/4" = 12.8 degrees
3/8" = 19.5 degrees
1/2" = 26.4 degrees
5/8" = 33.7 degrees
3/4" = 41.8 degrees
7/8" = 51.1 degrees
1" = 62.7 degrees
9/8" = 90 degrees
1/4" = 12.8 degrees
3/8" = 19.5 degrees
1/2" = 26.4 degrees
5/8" = 33.7 degrees
3/4" = 41.8 degrees
7/8" = 51.1 degrees
1" = 62.7 degrees
9/8" = 90 degrees
Turning it around, here are the from-contact-point distances for the cut angles divisible by ten:
0 degrees = 0"
10 degrees = .20"
20 degrees = .38"
30 degrees = .56"
40 degrees = .72"
50 degrees = .86"
60 degrees = .97"
70 degrees = 1.06"
80 degrees = 1.11"
90 degrees = 1.125"
10 degrees = .20"
20 degrees = .38"
30 degrees = .56"
40 degrees = .72"
50 degrees = .86"
60 degrees = .97"
70 degrees = 1.06"
80 degrees = 1.11"
90 degrees = 1.125"
OK, this is all well and good, but how can we actually make a usable aiming method out of it? Well, we don't have to use all those distances or be able to recognize all those cut angles. For example, in fractional-ball aiming, or SAM, or back-of-the-ball aiming, we generally use just a small number of reference aims -- 3/4-ball aim (14.5-degree cut), 1/2-ball aim (30-degree cut), 1/4-ball aim (48.6-degree cut) -- and then we use our feel or experience to aim a little thicker or a little thinner for shots between those reference points. So let's do something similar with distance-from-contact-point aiming.
We could, for example, use quarters of an inch from the contact point for our references:
1/4" = 13 degrees
1/2" = 26 degrees
3/4" = 42 degrees
1" = 63 degrees
These four references, along with 0" and 9/8" for the two extremes, would seem to give us a useful baseline of reference points that we could learn and then fine-tune in actual use to fill in the intermediate angles.1/2" = 26 degrees
3/4" = 42 degrees
1" = 63 degrees
Now, I fully appreciate that this method has some shortcomings that would make it undesirable for many (probably, most) people. It relies on identifying the contact point and then keeping that "in sight" long enough to identify another point a certain distance away from it -- and then keeping that new "invisible" point in sight as an aiming target. That is all complicated by the fact that any particular distance from the contact point appears smaller as the distance to the OB increases.
While this method will not be replacing my own current way of aiming, I thought it would be interesting to some people at least from an academic standpoint. And I wouldn't be surprised if it was actually helpful to someone as a real aiming method.