Hi Colin,
It's been really good to see you posting again over the last few weeks.
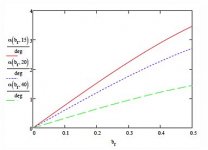
I'm not sure if this will address your question exactly, but according to Ron Shepard's derivation, and then Dr. Dave's (see below), squirt does increase nearly linearly with tip offset. If it was exactly linear, then the pivot point on the stick would remain fixed at one location. But it isn't, though close. On page 4 of Dr. Dave's treatment, he plots squirt vs tip offset for three different ratios of ball mass to shaft endmass (i.e., high squirt (red) to low squirt (green) shafts):
http://billiards.colostate.edu/technical_proofs/new/TP_A-31.pdf
View attachment 386865
You can see the squirt tailing off some with increasing offset. Therefore, the stick's pivot location should migrate down the shaft toward the butt, a little anyway, with increasing offset. I can't give you a hard figure as to how much, but remember Ron mentioning something like an inch or two. This would depend a bit on the particulars of a given shaft, I would think.
I'm afraid I'm going to have to avoid any discussion of such details as tip curvature/shaft diameter right now as I'm preoccupied with a problem jsp brought up in the other thread about limiting cueball travel. Patrick and I have sort of hashed over this in the past, and I think the upshot is that they're irrelevant given the definition of a shaft's pivot point. But maybe Dr. Dave or Patrick will take notice and chime in?
Jim
Thanks Jim,
That helped get my cogs turning. I recall reading Dr. Dave's stuff years ago but had forgotten about it.
One thing I notice is that I think that chart is a bit off, as my pivot point, which is medium deflection (11.8mm diam) is about 12 inches, which equates to about 3.5 degrees at 0.5 diameter (18.5mm) tip offset, which puts my cue on the red line.<-- (I question this below)
I did some math on offset v pivot angle. If it were a line intersecting a flat surface, it would be almost linear over 3-4 degrees with the same curve as the graph you posted. It would asymptote at 90 degrees.
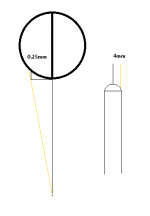
However, two factors affect this path. The most significant is that the cue tip contact point shifts approximately 4mm over journey to approximately 18mm max offset at about 3.5 degrees. That's reduces the gradient of the line by about 22%.
The other factor is that the surface is getting further away. At 18mm offset, the surface is about 4mm further away. This increase the offset by about 0.25mm for the given pivot angle of approx 3.5 degrees. This reduction is about 1.4%, so it is far less significant than the effect of tip curvature.
Let's say 22% -1.4% is approximately 20%. This suggests that the gradient is about 20% less if pivot angle is charted on the y and tip offset distance is charted along x, compared to Dr. Dave's chart.
The main thing is that both of these appear to track almost linearly and with almost identical curves, such that the pivot point would seem to be pretty fixed for all offsets.
However, thinking around this full circle, makes me question my earlier argument, as it would suggest, if I've got it right, that the pivot point would be about 20% longer if we used a line on a flat surface, and so my 3.5 degree max offset is really only effectively 2.8 degrees, mainly due to the shape of the tip. That places my cue on the blue line on Dr. Dave's chart, not the red line.
Still wrapping my head around it a bit, but I find it useful to write it down.
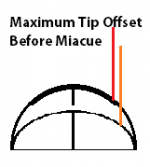
Attached image may help others to perceive the 2 factors I discussed.
Edit: Something I just thought to add. Each mm of reduction of tip diameter should reduce the offset adjustment by about 0.4mm, this would increase the pivot point length by about 10%, even with the same tip end mass. i.e. Approx 1 inch in most cases. The reduction of tip end mass for a 1mm reduction in diameter is approximately 20%. These are accumulative, such that reducing a 13mm tip to 12mm or a 12mm to 11mm increases the length of the pivot point by about 30% or about 3 inches.
Colin