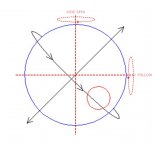
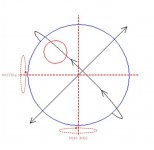
I've been trying to understand how side spin interacts with backspin or roll on the cueball. Imagine you have a geographic globe in your hand, and you spin it clockwise. Now imagine that, while it's spinning, you turn it upside down. It's now spinning counterclockwise. In this example, a 180 degree "roll" of the sphere has the effect of reversing the direction of the spin as well, relative to its surroundings.
My question is this: when you strike the cue ball with side spin and either top or bottom english, how is it possible to predict the effect of the side spin when the cue ball encounters a rail or another ball? For example, if you hit the ball with left spin and the cue ball rolls exactly 180 degrees before hitting a rail, you'd think it would behave as though you put right hand english on it instead, right? And yet, the effect of left or right english seems to be predictable regardless of cue ball roll or backspin.
I realize that this is a largely theoretical question that probably won't affect how anyone plays the game, but it's been bugging me. Come to think of it, though, I sometimes do have a shot where the cueball comes off the rail at an angle that seems to be opposite of what I would have predicted--I used to just pass it off to user error, but now I'm wondering. Can anyone explain this?
My question is this: when you strike the cue ball with side spin and either top or bottom english, how is it possible to predict the effect of the side spin when the cue ball encounters a rail or another ball? For example, if you hit the ball with left spin and the cue ball rolls exactly 180 degrees before hitting a rail, you'd think it would behave as though you put right hand english on it instead, right? And yet, the effect of left or right english seems to be predictable regardless of cue ball roll or backspin.
I realize that this is a largely theoretical question that probably won't affect how anyone plays the game, but it's been bugging me. Come to think of it, though, I sometimes do have a shot where the cueball comes off the rail at an angle that seems to be opposite of what I would have predicted--I used to just pass it off to user error, but now I'm wondering. Can anyone explain this?