Close ball separation angles, half distance passing point, and the secant function
It's a bit difficult to make shots where the balls are close together and I got curious about the maximum cut angle available. I broke out the graphing stuff and discovered some interesting things about the relationship between the separation of the balls and the maximum angle you can get. I found that the secant function will give the MAX cut angle and the point half way between the balls centers can be used to fine tune the shot line for those close in shots. (DD)? I'll explain the trig behind the ball geometry later in the post for those that are interested in the math.
In the first column, S is the separation in ball diameters. The second column is the MAXIMUM cut angle available. Since the data is in ball diameters it's valid for any two balls of the same size. (snooker, bowling, bb, marbles, etc.) The last column is the ball separation in inches and it's for standard 2 1/4" balls only.
For balls with less than 1 diameter separation
Separation: Max
S = 0 : 0 , Frozen Balls
S = 1/8 : 27 , .28" (> 1/4")
S = 1/4 : 37 , .56" (> 1/2")
S = 3/8 : 43 , .84" (< 7/8")
S = 1/2 : 48 , 1.125" (1 1/8")
S = 5/8 : 52 , 1.40" (> 1 3/8")
S = 3/4 : 55 , 1.69" (< 1 3/4")
S = 7/8 : 58 , 1.97" (< 2")
For balls above 1 diameter separation
S=1 : 60
S=2 : 70
S=3 : 75
S=4 : 78
S=5 : 80 This is about one diamond separation on an 8' table ( 1' per diamond is 5 1/3 balls)
S=6 : 81
S=7 : 83
S=8 : 84
S=9 : 84
S=10: 85 About 2 diamonds separation
S=15: 86
S=20: 87 About 1/2 table
S=25: 88
S=43: 89 (MAX=88.7) This is the length of 8' table ( 42 2/3 diameters)
S=48: 89 (88.8, 9' table)
S=53: 89 (88.9, 10' table)
S=70: 89 (89.2, 12' snooker table with 2 1/15 balls)
The table shows that the MAX angle grows very quickly from no separation out to one ball diameter. Then it slowly becomes more even (linear) as the separation gets larger. You should remember that the MAX angle is the thinnest cut possible, a '90 degree' cut at the extreme edge of the object ball. On the table you'll probably only be able to get within 5 - 10 degrees of the MAX angle due to the difficulty of the cut.
I got the data by looking at the internal tangent lines between two balls. I examined a lot of diagrams and found the secant function made all the pieces fit together. Looking at the point where the tangents intersect notice that it's at the midpoint on the center to center line. The line segment from the midpoint to the ball center is the secant line. Notice the secant line is the same for both balls. The balls are separated by two radii and two equal line segments that 'jut out' of the balls. Since two radii are one diameter and two equal extra pieces of radii are equal to one extra diameter piece, the separation can be expressed in diameter units.
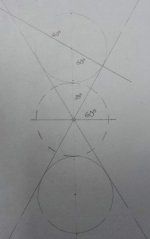
The MAX angle is found by using the internal tangent lines as shown in the diagrams. The internal tangent lines will define the part of the object ball which can be hit due to the separation of the balls. The angle the tangent line forms when it crosses the center line between the balls is the compliment (90*-x) of the secant angle. The value of the secant angle will give the distance between balls in 'diameter' units. Here's a few more diagrams with 1/4, 1/2, and 2 ball separations.
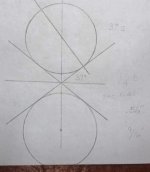

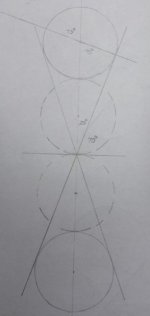
Using the above information a simple equation can be written to find the MAX angle as a function of ball diameters or the distance between the balls. The equation for Max angle if the separation S is in ball diameters : MAX = arcsecant [S + 1].
The equation for finding MAX if you know the distance between the balls is : MAX = arcsecant [1 + (d/D)] where d is the distance between the balls and D is the ball diameter.
As an example, for a distance of 1 inch using 2 1/15" snooker balls (31/15") : MAX = arcsecant [1 + (1 / (31/15))] = arcsecant [1 + .484] = 47.6 rounded down to 47 degrees.
-----------------------------------------------------
The half distance passing point may be related to double distance aiming or it may BE DD. I don't know enough about the system to be sure. In the diagrams notice that the edge of the cue ball will roll over the midpoint ( call it MP ) to make a 90* cut. Also the center of the cue ball will roll over MP to make a 0* cut. This implies that the point of the cue ball that rolls over MP will be the point that makes contact with the object ball. The MP is pretty easy to find when the balls are tight and it provides an extra check on the alignment. Once the contact point on the CB is found it can be aimed at MP. If it rolls over the MP it will hit the contact point on the OB and the ball will drop. It's a handy aid and easy to use. It works well for those close ball edge to edge shots.
It's a bit difficult to make shots where the balls are close together and I got curious about the maximum cut angle available. I broke out the graphing stuff and discovered some interesting things about the relationship between the separation of the balls and the maximum angle you can get. I found that the secant function will give the MAX cut angle and the point half way between the balls centers can be used to fine tune the shot line for those close in shots. (DD)? I'll explain the trig behind the ball geometry later in the post for those that are interested in the math.
In the first column, S is the separation in ball diameters. The second column is the MAXIMUM cut angle available. Since the data is in ball diameters it's valid for any two balls of the same size. (snooker, bowling, bb, marbles, etc.) The last column is the ball separation in inches and it's for standard 2 1/4" balls only.
For balls with less than 1 diameter separation
Separation: Max
S = 0 : 0 , Frozen Balls
S = 1/8 : 27 , .28" (> 1/4")
S = 1/4 : 37 , .56" (> 1/2")
S = 3/8 : 43 , .84" (< 7/8")
S = 1/2 : 48 , 1.125" (1 1/8")
S = 5/8 : 52 , 1.40" (> 1 3/8")
S = 3/4 : 55 , 1.69" (< 1 3/4")
S = 7/8 : 58 , 1.97" (< 2")
For balls above 1 diameter separation
S=1 : 60
S=2 : 70
S=3 : 75
S=4 : 78
S=5 : 80 This is about one diamond separation on an 8' table ( 1' per diamond is 5 1/3 balls)
S=6 : 81
S=7 : 83
S=8 : 84
S=9 : 84
S=10: 85 About 2 diamonds separation
S=15: 86
S=20: 87 About 1/2 table
S=25: 88
S=43: 89 (MAX=88.7) This is the length of 8' table ( 42 2/3 diameters)
S=48: 89 (88.8, 9' table)
S=53: 89 (88.9, 10' table)
S=70: 89 (89.2, 12' snooker table with 2 1/15 balls)
The table shows that the MAX angle grows very quickly from no separation out to one ball diameter. Then it slowly becomes more even (linear) as the separation gets larger. You should remember that the MAX angle is the thinnest cut possible, a '90 degree' cut at the extreme edge of the object ball. On the table you'll probably only be able to get within 5 - 10 degrees of the MAX angle due to the difficulty of the cut.
I got the data by looking at the internal tangent lines between two balls. I examined a lot of diagrams and found the secant function made all the pieces fit together. Looking at the point where the tangents intersect notice that it's at the midpoint on the center to center line. The line segment from the midpoint to the ball center is the secant line. Notice the secant line is the same for both balls. The balls are separated by two radii and two equal line segments that 'jut out' of the balls. Since two radii are one diameter and two equal extra pieces of radii are equal to one extra diameter piece, the separation can be expressed in diameter units.

The MAX angle is found by using the internal tangent lines as shown in the diagrams. The internal tangent lines will define the part of the object ball which can be hit due to the separation of the balls. The angle the tangent line forms when it crosses the center line between the balls is the compliment (90*-x) of the secant angle. The value of the secant angle will give the distance between balls in 'diameter' units. Here's a few more diagrams with 1/4, 1/2, and 2 ball separations.



Using the above information a simple equation can be written to find the MAX angle as a function of ball diameters or the distance between the balls. The equation for Max angle if the separation S is in ball diameters : MAX = arcsecant [S + 1].
The equation for finding MAX if you know the distance between the balls is : MAX = arcsecant [1 + (d/D)] where d is the distance between the balls and D is the ball diameter.
As an example, for a distance of 1 inch using 2 1/15" snooker balls (31/15") : MAX = arcsecant [1 + (1 / (31/15))] = arcsecant [1 + .484] = 47.6 rounded down to 47 degrees.
-----------------------------------------------------
The half distance passing point may be related to double distance aiming or it may BE DD. I don't know enough about the system to be sure. In the diagrams notice that the edge of the cue ball will roll over the midpoint ( call it MP ) to make a 90* cut. Also the center of the cue ball will roll over MP to make a 0* cut. This implies that the point of the cue ball that rolls over MP will be the point that makes contact with the object ball. The MP is pretty easy to find when the balls are tight and it provides an extra check on the alignment. Once the contact point on the CB is found it can be aimed at MP. If it rolls over the MP it will hit the contact point on the OB and the ball will drop. It's a handy aid and easy to use. It works well for those close ball edge to edge shots.