Following up on the discussion in this thread, I've completed what I believe to be an accurate plot of travel distances for the Cue Ball and Object Ball for the full range of cut angles.
I've chosen 12 as the base unit. That could be 12 diamonds, 12 feet or 12 inches. I chose this because it is quite typical distance and it divides well for some easily memorized rules of thumb.
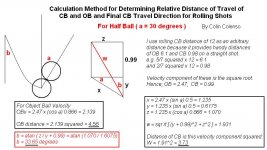
eg.For a rolling ball that would travel 12 feet unobstructed, if it hits an object ball full in the face at the beginning of its journey, it will hit the object ball 6.1 feet, approximately 1/2 and the Cue Ball will roll forward 0.98, or approximately 1/6th the distance the OB will travel.
This 1/6th ratio is very useful as a guide when playing rolling pots. For example, when you want to roll a straightish pot in, and the pocket is 3 feet away, you would likely aim to hit with a rolling distance of about 4 feet. If you can hit the OB that far, the CB will roll very close to 4/6th of 1 foot = 8 inches. 8 foot OB would be 8/6ths or 16 inches. These are the distances from where the CB was upon impact.
The chart below provide us with some other useful rules of thumb.
1. A hit of about 33 degrees (slightly thinner than 1/2 ball) will make the CB and OB travel the same distances. This can be a handy guide for hooking opponents.
2. From full to 3/4 ball hit (approx 14 degrees) the CB will only change from 1 up to about 1.8 feet for the OB travelling 6 feet. That's 1/6th to a bit less than 1/3rd. So by judging the fullness of shot, as compared to Full ball and 3/4 ball, you should be able to estimate CB travel distance to within a couple of inches. eg. 10 degrees will be around 1/4.
Thanks to JAL, Dr. Dave, jsp and others for helping me work this out.
Note: Calculation method is shown in post #22 below. Click here to go straight to it.
Colin
I've chosen 12 as the base unit. That could be 12 diamonds, 12 feet or 12 inches. I chose this because it is quite typical distance and it divides well for some easily memorized rules of thumb.
eg.For a rolling ball that would travel 12 feet unobstructed, if it hits an object ball full in the face at the beginning of its journey, it will hit the object ball 6.1 feet, approximately 1/2 and the Cue Ball will roll forward 0.98, or approximately 1/6th the distance the OB will travel.
This 1/6th ratio is very useful as a guide when playing rolling pots. For example, when you want to roll a straightish pot in, and the pocket is 3 feet away, you would likely aim to hit with a rolling distance of about 4 feet. If you can hit the OB that far, the CB will roll very close to 4/6th of 1 foot = 8 inches. 8 foot OB would be 8/6ths or 16 inches. These are the distances from where the CB was upon impact.
The chart below provide us with some other useful rules of thumb.
1. A hit of about 33 degrees (slightly thinner than 1/2 ball) will make the CB and OB travel the same distances. This can be a handy guide for hooking opponents.
2. From full to 3/4 ball hit (approx 14 degrees) the CB will only change from 1 up to about 1.8 feet for the OB travelling 6 feet. That's 1/6th to a bit less than 1/3rd. So by judging the fullness of shot, as compared to Full ball and 3/4 ball, you should be able to estimate CB travel distance to within a couple of inches. eg. 10 degrees will be around 1/4.
Some useful rules of thumb are:
Full Ball = 1/6
5 degrees = 1/5
10 degrees = 1/4
15 degrees (slightly thinner than 3/4 ball) = 1/3
20 degrees = 1/2
33 degrees = 1
45 degrees (slightly thicker than quarter ball) = 2:1
60 degrees = 6:1
These relate to the proportianal travel distances of the CB and OB.
Full Ball = 1/6
5 degrees = 1/5
10 degrees = 1/4
15 degrees (slightly thinner than 3/4 ball) = 1/3
20 degrees = 1/2
33 degrees = 1
45 degrees (slightly thicker than quarter ball) = 2:1
60 degrees = 6:1
These relate to the proportianal travel distances of the CB and OB.
Thanks to JAL, Dr. Dave, jsp and others for helping me work this out.
Note: Calculation method is shown in post #22 below. Click here to go straight to it.
Colin
Attachments
Last edited: