LAMas,
I'm running out the door, but I read your post. I'll clarify what I'm getting at later. I'm trying to tie in the pivot relationship with ghostball and other systems. I've got a few thoughts I would like to discuss and expand on your method possibly. Hence, all my questions.
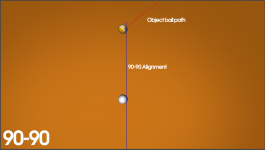
One thing jumps out at me with your answer. 90/90 does not vary the bridge length or use any CP at all in its setup. You must use a consistent bridge distance and vary the 3 aiming points on the OB (edge, center, opposite edge) not use a CP (as in ghostball aiming). There is some adjustment or tweeking only on very close to OB shots which is done with almost all systems.
Mike,
I thought that I understood 90/90 from dr_dave's colostate diagrams, but you say that I don't.
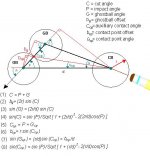
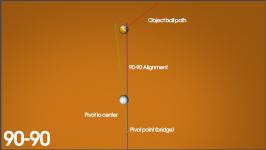
The diagram shows the aim prepivot to be the obverse CP on the OB and a corresponding obverse CP on the CB. This is results for a single trajectory after the pivot as drawn. if you move the OB down table, the CB will eventually roll past the OB to the left. This is diagramed from a top view and is dimensionally accurate.
Things change with perspective when you are down on the shot/table; the CB will appear smaller than 2.25" and the OB will appear eve smaller than the CB etc.....but you already knew that.
In order to satisfy the diagram, you must point the tip of the cue and the length of the cue (at the obverse contact point) at the CB toward the vanishing point.
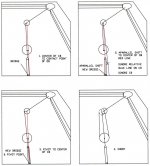
After the first alignment, one pivots to the center of the CB and shoots to the GB location....how it works for this cut angle at this distance between the CB and OB.
This makes sense to me from the info given, but you say that there is more to learn as you understand 90/90.
Are you going to proffer your interpretation to this august though tiny audience?
Thanks.
Last edited: