Huh?...SPF=randyg
Randy...Simply put....SAM 3 and SAM 4.
You're welcome!
Steve
Huh?...SPF=randyg
Well why didn't you just say that???!!!J/K. The next question is how do you learn to shift the correct x distance? You could use feel, but the pivot flamers would have your head. You could use a headset from a helicopter gunship to super-impose coordinates on the CB/OB or...wait a minute!!!...you already have a product ready to market. IIRC your line of work deals with laser guidance for armament systems. Is this thread a marketing initiative for a new pool aiming gizmo? If it is I will buy the first one!:grin-square:
All kidding aside, with any aiming system you have to be able to repeat the process. What have you done to make this happen?
Best,
Mike
Can't say I've tried it LAmas. I trust what geometry has to say, even when I'm the one doing it.I know what you are sayin, but at the table, if I aim a dowel at the near end of the table (cue) at the right edge of the OB down at the far end of the table, and then roll the dowel to the left until it is aimed at the center of the small appearing OB, Then the amount that I roll the dowel (parallel?) is very small and nowhere close to the center of the CB.
Rolling the dowel is a parallel roll and one would expect that the dowel rolled as described above would now be centered on the CB....But it isn't...go figure...counter intuative...optical illusion?
It works for me though.
Tried it at the table?
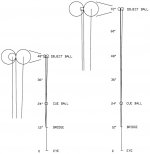
Jal,
Here is an Aparallel CTCP picture with 5X blow up of what I see with the smaller appearing OB at distance superimposed inside of the top view - why it works for all distances.
I have depicted a 90 degree cut at:
- The bridge remains in the same location
- Bridge 12" from the shooters cyclopsian eye.:wink:
- CB 12" from the bridge
- On the left, small appearing OB 24" (2 feet) down table from the CB.
- On the right, smaller appearing OB 48" (4 feet) down table from the CB
- Aparallel shift is small at 2 feet and smaller at 4 feet.
- The contact point (CP) on OB for cuts less than 90 etc., approach the center of the OB.
View attachment 139422
Acad is geometrically correct at all centers diameters and intersections etc.
I haven't studied the effect of different eye to bridge, bridge to CB etc., yet.
Thanks for your and mikjary's continued interest and look forward to your geometry.
LAMas,
I might not remember because you've covered so much ground on this proof, but a detail I thought about was the actual contact point versus the aimed contact point on the OB. We know about the ghostball meeting the OB at the CP and we are aiming at this point with the CB center. Since we already know the contact point one could say just shoot at it and forget the offset and pivot. But as we know this will not pocket the OB unless we allow for the added size of the CB to get to the ghostball position.
So further, the shift you are using equalling the aparallel line to center OB is also allowing for the additional size of the CB to achieve the ghostball position. Because if you actually pivoted back to the contact point you would not cut the ball thin enough.
Just a thought about what the shift is doing.
Mike,
You pivot back to the center of the CB as in CTE.
It is the contact/impact point that the ghost ball (GB) must impact to send the OB to the pocket. The system would be too difficult and vague if it were predicated on finding the GB center. If one can find the GB center then just shoot at it without the shift or pivot.
The nut is, when down on the shot, that once you determine where the CP is, you then "parallel" shift the cue and bridge to the center of the small OB. It is this calibrated shift that gives you a shot angle after you pivot, from your bridge, to the center of the CB. The CB then travels toward the OB (outside of the CP) and contacts the OB where the GB would/should.
The system thus "doubles the distance" from the CP to the center of the small OB. My problem with double distance aiming for cuts from 31 to 90 degrees is that the aim spot is off of the OB on the felt or rail etc..
I hope this helps.
Yes, I know about the pivot to center. I was making the point about aiming to the CP and the pivot taking you to the GB center. Is this a double the distance after the pivot?
Mike,
Yes, you are correct sir.
It is the parallel shift to the OB center that moves the bridge to the side to create one side of a triangle; the pivot back to the center of the CB creates the other side of a triangle (equilateral) with the third short side being equal to double the distance from the CP to the center of the OB;
Included in this short side is same distance from the CP to ther center of the OB but on the other side of the CP away from the center of the OB.
This then doubles the distance and is where the CB is sent at the shot.....to the required GB location.
Does this help a bit more?
Where is the doubled distance? Are you saying that you are doubling the numerical difference (1/8th ball, 1/3rd ball, etc.) or are you doubling the aparallel x distance? This is what I've been looking at and trying to point out about the pivot compensating for your smaller aparallel shift.
I tried it on my table, but I couldn't stop visualizing the double the distance out of habit. :grin:
Mike,
First, in my last diagram, do you recognize that there is a GB and a OB with a smaller OB inside that is touching the larger to the right at 3:00?
The smaller OB is the relative size from the "EYE" when down on the shot in perspective/fore shortened.
In this 90 degree cut example, the CP and 3:00 on both OBs just happen to be the same point.
The aparallel shift is shown on the smaller OB by the 2 verticle lines. The bridge, as a result is shifted away from the center of the CB by this small anount. The cue is then pivoted to the center of the CB which results in a line (from the top) to the base of the GB.
This is, thus, a way to create a path to the double distance location - regardless of the distance between the CB and OB.
Phrased differently:
The bridge has to move from the original CTCP line bridge location - or any pivot from that location would be back to the same location - center of the CB.
The aparallel shift (when down on the shot in perspective) that is established by sighting the center of the CB at the CP and then shifting to the center of the small OB down table creates the axis for an arc/pivot that when aimed back at the center of the CB (from the top view) is aimed at the center of the GB location. In order for this to be correct, it has to send the CB (from the top view) to the doubled distance.
It does get you to the double distance location for the GB...it is unfortunate that you know where that is and seem to say that you are jaded by that knowledge.
If you didn't know double distance or GB, you might hit the OB correctly with the CB and say WOW that shot fell into the pocket that I was aiming for.
You tried it and it seeems that the mechanics work...It works for me.
Don't ask me to give you the mathematics of the geometry next - I am not that interested in this academic discussion.
As I said before, I could teach it to my 10 year old Grand Daughter - perhaps quicker than "double the distance" or "ghost ball" which to me takes some imagination and not discreet points of aim as in Aparallel CTCP.
Next question before I get too drunk....:boring2:
Holy shit, let's just make some balls with the right speed control and either try to play position or safe. There might be some english in that equation somewhere also. That's about it.
LAmas, sorry for the delayed response (still learning Sketchup).Jal,
Here is an Aparallel CTCP picture with 5X blow up of what I see with the smaller appearing OB at distance superimposed inside of the top view - why it works for all distances.
I have depicted a 90 degree cut at:
- The bridge remains in the same location
- Bridge 12" from the shooters cyclopsian eye.:wink:
- CB 12" from the bridge
- On the left, small appearing OB 24" (2 feet) down table from the CB.
- On the right, smaller appearing OB 48" (4 feet) down table from the CB
- Aparallel shift is small at 2 feet and smaller at 4 feet.
- The contact point (CP) on OB for cuts less than 90 etc., approach the center of the OB.
View attachment 139422
Acad is geometrically correct at all centers diameters and intersections etc.
I haven't studied the effect of different eye to bridge, bridge to CB etc., yet.
Thanks for your and mikjary's continued interest and look forward to your geometry.


LAMas,Mike,
I'm not quite drunk so...
On any shot or cut down table. the included angle from the center of the CB to the center of the OB to the CP is smaller/narrower than when the OB is close to the CB.
I say this for in order to double the distance from the CP to the center of the OB, one has to take both into account. As the OB goes down table, that distance gets smaller due to perspective and the shooter has to deal with it - why far shots are harder than medium distances between the CB and OB.
I won't talk about the real close shots that you can't double the distance accurately.
Logic told me that in order to narrow the included angle from the center of the OB and its CP, I could/must respect/use the image presented by the smaller appearance of the OB to narrow the angle ...or the CB wil be sent away from the GB...what dr_dave has asked the CTE folks to solve and reveal.
It was you that pointed me to 90/90 and while playing around with that system, as I undertood it, that is a different pivot system that is based on a logical relationship to the CP and not to "one tip" or "1/2 ball" from CTEL that results in one aim/angle without secreted tweeking.
Though 90/90 doesn't have the center of the OB as part of it's equation, it has a variation of bridge distance from the CB for different distances between the CB and OB that is, to me, inconvenient and vague.
In Acad, the relationship was linear i.e., the OB is perceived as 1/2 the diameter of the CB when the CB is the same distance from the eye - 2 feet from the eye to the CB and 2 feet from the CB to the OB and 1/4 the diameter when the OB is 4 feet away from the CB.
Since this is a linear relationship and constant...so will the distance from the CP to the center of the smaller OB be proportionally smaller.
With these assumptions. I did some "what if scenarios", in Acad, with aparallel shifting using these two discrete points (CP and center of OB [regardless of feature size]) and a one foot distance for the bridge behind the CB; and the intersect from the GB to the center (from above) of the CB resulted in the eye being 1 foot behind the bridge.
I then went to the table and did imperical testing to validate the geometry.
I will not put in the many hours to get proficient at this A'CTCP method for "double the distance" is more parsimonious, but like CTE, it is a method of teaching a novice another way to address a shot.
Thanks for your persistance....now where's that cold one?
It took me several college degrees to learn this ... try scratching. :grin:
Dave
LAmas, sorry for the delayed response (still learning Sketchup).
I appreciate the meticulous care with which you've made your drawings and I understand what you're trying to illustrate. It's very clear that the parallel offset to OB center is different at the two different CB-OB separations...in the drawings. But there's a problem.
Overall, your diagrams consist of a top view 'orthographic projection' (I think that's the right term). But you're also mixing in a perspective projection as well by using the "proportionately" smaller OB. That's sort of mixing apples and watermelons. In the top view, to be fair, the OB would have to be the same size as the CB.
On the other hand, if the diagrams were a perspective view, then true parallel lines with respect to the cloth/table would appear to be converging forward in the image plane (the screen in this case and as per my earlier diagrams...I know you know). If in this perspective view (large CB, small OB), you drew them as parallel in the image plane, then moved the camera to an overhead position and switched to and orthographic view (see below), you would see them as diverging in the forward direction. Rearward then, they would converge at a point. Here are those diagrams, though they're not of any particular shot, unlike yours.
These lines look reasonably close to parallel (best I could do) from the shooter's point of view (image plane):
View attachment 139496
The same diagram (unmolested) from the top view:
View attachment 139497
As indicated in an earlier post, that point where they meet (not shown above) depends on where your eye is positioned, which can be variable, and is in fact variable for different cut angles and CB-OB distances if you want to perform the final pivot to CB center (CTCP) at a fixed distance behind it.
Which view represents reality, the top one or the shooter's? I think the balls care about the relative positions of things on the cloth, i.e., as seen from above. No?
Back over to you.
Jim
(I haven't had a chance to read the exchanges between you and Mikjary yet).