If I understand the meaning of "fullness" in the table, then it seems to approximately agree with the other two: .9 fullness ~= .99 energy transfer, .8 fullness ~= .95 energy transfer. That's about a quarter inch and half inch, right?To look at the original question slightly differently, just consider the energy transfer from the cue ball to a single ball. The nature of that is not going to be much different from hitting a full rack. This simpler problem was solved a long time ago:
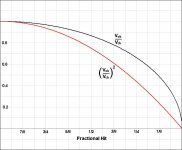
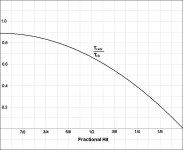
The velocity of the object ball is proportional to the cosine of the cut angle and the velocity remaining on the cue ball is proportional to the sine of the cut angle. What we are mostly interested in is energy transfer, and energy is proportional to the square of the velocity. Here is a table for various cases:
View attachment 209055
So for a 15-degree cut (about a 3/4-full hit) 93% of the energy is transferred into the object ball leaving 7% on the cue ball.
In fact the transfer of energy into a single ball is more efficient than into the rack as you can see by the fact that the cue ball bounces back after hitting a full rack -- it takes some energy away when it bounces back.
On the last note, yes, I am told that the transfer is less efficient due to the difference in masses of the cue ball v. the total mass of the rack. But I guess the interesting thing is the % of potential transfer given the masses involved.