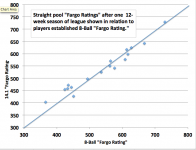
I understand that Fargo Ratings are not used for 14.1 (straight pool). If this is true, why not? Is there a universally accepted rating system for 14.1?
Thanks,
Will
Mike Page correct me if I'm wrong....
Fargo Ratings are based on whole games won or lost, not points won in a particular game. Games such as 14.1 and Banks do not have clearly defined winning objectives. You can play to any predefined score. Even if a score was mandated for Fargo entry for these games (eg. race to 25 points), the games usually take a lot longer to play than a single game of 8, 9, or 10 ball. For that reason, the game of One Pocket also can't be used. The Fargo Rate formula needs the varying game units to be roughly equivalent.
Oh, and the Fargo Rate formula, just like APA's Equiliizer formula, Weight Watchers points formula, etc. are all proprietary formulas. That's how they make their money.
Last edited: