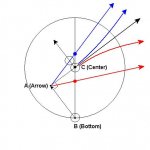
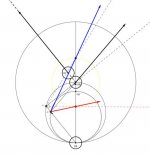
That's really interesting. Can you post your math for this as well? Based on your diagrams I believe I can ascertain the formula which leads to your conclusion, but I am having trouble quantifying the CB spin based on the tip location. I don't believe the relationship between tip position and CB spin is entirely linear, due to the inelastic nature of the tip and CB collision. In addition I think many of the factors in the tip/CB collision would make quantifying this spin extraordinarily difficult, such as tip end mass, tip shape, and tip frictional co-efficient.
OnTheMF, thanks for your interest. My apology, but I really don't have the time at the moment to go into all the math. Dr. Dave's material has/can likely answer most or all of your questions. Since he's looking into this, I don't know, but he may eventually put up one of his technical proofs on the subject.
Even if we assume a perfectly elastic collision for the stroke, and a linear relationship between tip position and CB spin, it seems in your diagrams that CB speed is not a factor either. This is definitely a departure from the standard thinking on throw, unless I have been dreadfully misled

As it happens, the indicated correction (using the vector from the (3/5)R below center offset) works regardless of the actual amount of throw. So it is CB speed/surface condition independent. You could always add more vertical offset to compensate for the frictional loss of spin during the collision, but that
would depend on CB speed and cut angle (i.e., coefficient of friction). The inside english adjustment doesn't.
If your math checks out, it will definitely change my game.
But which way?

I was expecting the line depicting the tip position for zero throw to be parabolic (or perhaps circular), returning to the vertical centre at 3R/5 above the horizontal centre. Clearly that kind of thinking would have me adjust in the wrong direction for follow cut shots.
I have to confess, I'm not completely following this.
I'll truly try to answer any questions, supplying the math as necessary (in addition to Dr. Dave's) shortly. Very briefly, the CB's velocity at roll after the collision is derived from the general relation:
Vroll = (5/7)[
Vi - (2/5)
WXRb]
where
Vi is its initial velocity,
W its spin, and
Rb the vector from the center of a uniform sphere to the point of contact with the surface. This can be derived in various ways, and it sounds like you might already be familiar with it.
The CB's spin about the horizontal axis (X R) is given by:
RWx =-5/2(Bz/R)V
where Bz is the vertical offset, R the ball's radius, and V its speed.
If we set the y-axis (unit vector
j) along the cueball to ghostball direction, with x-axis to the right (unit vector
i) for a cut to the left, then using the above relations, the cueball's velocity after the collision and natural roll sets in is:
Vroll = (5/7)[Vsin(C)cos(C)
i + (Vsin^2(C) + (Bz/R)V)
j]
where V is its pre-impact speed in the
j direction and C the cut angle.
However, it's better to express the unit vectors
i and
j in terms of a unit vector along the tangent line
t and one along the object ball-ghostball line of centers
n:
i =
tcos(C) -
nsin(C)
j =
tsin(C) +
ncos(C)
Substituting these in the expression for
Vroll and a little algebra, you get (I hope!):
Vroll = (5/7)(V/R)[Rsin(C)
t + Bz
j]
(Note that
j reappears in this final expression by combining terms.)
Thus, if you scale V to a ball's radius, the CB's final roll direction is the vector sum of Rsin(C) along the tangent line and the vertical tip offset in the cueball-ghostball direction.
Sorry, but I have to run. Hope that illuminates something.

Jim