I intentionally mistyped that just to see if you were paying attention...yeah, that's what happened...I see the logic and agree with the modification. But the "sin(cut angle)" threw me off for a while - shouldn't that be cos(cut angle)?
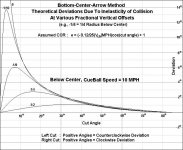
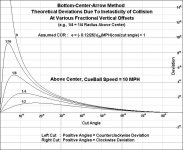
That's actually Coriolis' "alpha", not mineOne difficulty in easily accounting for inelasticity is that the coefficient of restitution (I realize your "alpha" isn't the COR, directly) varies, I believe, with the CB speed component along the impact line. Thus, so will alpha. I'm basing this on tests done by Cushioncrawler (Cue Chalk Board). I have them on another semi-defunct computer, but I believe I remember that the greater the speed, the smaller is the COR. This, of course, makes it cut angle dependent as well.
He didn't describe any experiments attempting to establish the validity of that assumption, but I'm sure he was aware it was an approximation that was useful for introducing the idea graphically into the constructions of how the ideal case is affected. Remember, his constructions were there to help guide the lay reader's intuitions in support of the introductory summary section of the book. (Interestingly, he did describe experimentally suspending cues and balls from cords to attempt measurements from controllable tip/ball collisions, but he lamented the slower-than-actual-play max cue speeds he could attain that way.)
Yeah, Coriolis totally missed the ball when it came to squirt. It's one of the reasons I suspect that he wasn't such a good player himself to have missed it. It's painful with our current understanding to read his argument about how if the cue stroking line and the CB path weren't parallel, it would be "impossible to play with any confidence...but we recognize from experience that the two directions are in fact the same." As Dr. Dave once said, "Coriolis was brilliant, but he didn't have a high speed camera."Dr. Dave has described the departures from the predictions as well. I think a significant one is squirt. Although it may be relatively small in the inclined plane of the cue, it's projection onto the horizontal plane magnifies it considerably at the steep inclinations used with masse shots.
Jim
Robert