Earlier I said:
If this is the situation described by your example (Dr. Dave's):
]///////////(mass 1)<----- Force----->
(mass 2)
then the force is pushing on the wall behind the spring besides compressing it. Without the wall (the support), there is no compression. So the analogous "endmass" here is mass1 plus the wall plus whatever it's attached to.
Hi Corwyn,
Sorry for the delay! I was just referring to the spring as a "massless" conveyer of any momentum of mass 1 toward the wall. My point was that the wall should be included as a part of the "endmass" in my analogy. In other words, for the tip-cueball collision, any part of the shaft that gets pushed to the side should be deemed as 'endmass.' As such, there are no forces acting laterally on the cueball (i.e., restoration forces) that aren't attributable solely to the displacement (momentum) of that endmass. However...
Dr. Dave has been arguing, as illustrated by TP B.19, that the sideway's forces on the cueball stem from both endmass and the cue's stiffness (restoration forces), although the latter are relatively small. This was the source of our disagreement.
First though, as an aside, one thing you really have to like about Dr. Dave is that he never throws his authority at you. He brooks arguments and even solicits critiques of his work from those of us with only a tiny fraction of his education. He treats you essentially as if you are his peer.
He called me a few days back explaining his position, which, I'm afraid, only half-registered and which was subsequently dismissed by me as I reverted to the view indicated above (it's all endmass!) But then he very patiently tried once more and, finally, it's begun to sink in. This is my understanding of the conversation and I hope I'm not distorting his words (too much

).
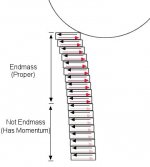
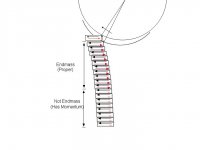
As the transverse (shear) wave travels down the shaft, it has to be reflected back off the medium in which it's propagating and reach the tip again in order to be felt by the cueball. If you divide the shaft into thin sections, when the wave reaches an interface between two sections, the leading section first transmits the shear force to the trailing section. The trailing section then, naturally (Newton's Third), produces a reaction force, equal an opposite, which then travels as a wave (disturbance) back toward the tip. Here's sort of an illustration with the black arrows indicating the original shear and the red ones indicating the reactions.
View attachment 410832
Note: Maybe I should have reversed the locations of the black and red arrows in each section for better clarity.
As you get farther down the shaft, there isn't enough time for the reflected waves to return all the way to the tip. This is indicated by the pale red arrows. However, in this region, the sections are 1) moving to the left (have momentum), and 2) the reaction forces they're generating, while not reaching the tip, are slowing down the upper section whose reaction forces are reaching the tip.
Therefore, since we define "endmass" to be the mass that, from being pushed aside, produces a counter-force that acts on the cueball, only the upper section fits the bill. It (the upper section), being slowed by the reaction forces from the lower section, does not posses all the equal-and-opposite momentum of the cueball - the lower section carries part of it. Thus, there must be more force acting on the cueball than we can account for from the endmass (proper) alone. That force must be the restorative (flexing) force generated by the bend, since the lower section can't contribute - its waves never reach the tip.
Well, I hope I have that right, at least in spirit, and want to heartily thank Dr. Dave for taking the time to go through this with me several times!
Jim