Statistics and pool

[mr5994]

There are a lot of great, simple ideas from statistics that can be used for pool. For instance, if you are slightly better than another player (or versa vice) what are the odds of winning a race to something?

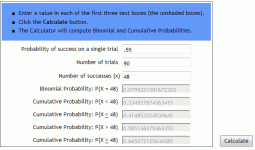
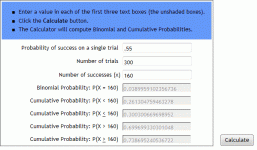
Suppose they are slightly better than you...let's say 55% of the time they'll win a game. That'd mean that you'd have a 45% chance, which doesn't sound all that bad, does it? But in a race, the probabilities are added. The longer the race, the less chance you'll win it! In a race to 8, for instance, they are likely to win a little better than 65% of the time.

If you want to know how to calculate for other races, or different probabilities, the relevant mathematics is here:

http://nrich.maths.org/353/solution

You could, of course, hope they have a bad day, and you have an exceptional one....

If there is enough interest in this kind of thing, I'll post how to use statistics to predict high runs based on average runs, or the likelihood of making a certain number of balls on the break, based on your average number of balls made on the break.

The binomial distribution can be used to model all of the examples you've listed.

With all of the posts on breaking Mosconi's 526 run, one interesting application would be the liklihood of a current top player beating the record. If we know the probability that John Schmidt will run a single rack, we could use the binomial distribution to estimate the probability that he would run enough racks to beat the record. I would guess 526 is not as unreachable as most people think.

 

[Bob Callahan]

The binomial distribution can be used to model all of the examples you've listed.

Yep. I was trying to avoid technical terminology. For folks who don't want to drag out a calculator and work through the steps given in the link in the first post, there's an easy-to-use, online, handy-dandy calculator:

http://stattrek.com/tables/binomial.aspx

Here's how you'd use it to compute my initial example:



The last line is the one we're interested in.

 

[Siz]

Not sure I get this.

Suppose I have 2 cues, a break cue and a playing cue. But when I leave the house I only take one of them, chosen at random.

When I play using the break cue, I lose every rack. But when I use the playing cue, I win every rack.

After a large number of trials, the stats show that I win 50% of games.
What is the probability that I win 10 games in a row? (And what does a binomial distribution predict?)

Same question, but instead of 2 cues, half the time I go out with my 'pool head' on, and half the time I go out preoccupied with something else.

Or, if I win the first rack, I get confident and play well. But when I lose the first one, I go to pieces.

Etc (you can tweak the scenario to make it more realistic).

But perhaps where the stats are available, ie for pro games, they show that the individual racks act as if they are independent? If so, a reflection of the mental discipline needed to be a pro?

 

[jason]

.

My son majored in math and works with statistics. He follows sports and analyzes a lot of the data. He claims there is no such thing as a clutch hitter in baseball. It is just something people like to imagine or talk about.

.

I will politely disagree.

I'm not surprised by your sons view point especially considering his background and education. I will agree that there are no hot or cold streaks in gambling such as craps or roulette or something of that nature. They are imagined.

As someone who has played a lot sports in life, I truly believe there is a such thing as being clutch. The variable that makes the difference is the human element. Not every human being reacts the same to the same circumstances. Not every human is made up of the same stuff. Adrenaline is released and focus and concentration sharpened.

There are a lot of factors that make up an individual. Some men will run into a burning building while some will run away. My point is under intense pressure some people have fight and some people flee. Some people step up to the plate. I think it takes pressure situations to bring out the best in some people.

I will also agree that some people are chokers as well. How many people have you seen over the years that consistently miss the eightball more than any other ball? Plenty I'm sure.

JMO

 

[iba7467]

The problem with the mental side is that its really hard to measure and observe. If we just go from the things we can observe (statistics) we can usually predict pretty well the likely range of outcomes (probabilities). Statistics can also tell us whether the events are independent. As far as top-level 9-ball play goes, what has been reported from the statistics is that the breaker does not win more than about 50% of the time. Statistically, there seem to be no more streaks than you would expect from a random number generator set up with the same probabilities. At basketball, the "hot hands" phenomenon was studied and the result was that there is no "hot hands" phenomenon.

Kobe Bryant's 83 points was not statistical. You could certainly argue that Wilt's was because of his often high numbers, but nothing would explain Kobe's performance.

Also, athletics is much more dependent on human beings than true odds which makes every application very questionable.

Another major thing that many people do not understand is that gambling should be based on medians not means (similar to home prices). Let's use the example of playing rotation. Let's say a player runs 1,1,4,4,15 balls. His average is 5 balls. Acording to the average a fair bet would be 6 is a win and 4 is a loss, but we can see that the guy would be -3 in this instance. If however you used the median which is 4, then a fair bet would be 5 is a win and 3 is a loss. In this instance he would be only -1 which is much more likely a fair estimate over the long run.

 

[Bob Callahan]

Sigh. Of course, in this kind of analysis, we're making some assumptions: Humans are consistant, and we actually know how much better one player is than another. You may have heard the, "Assume a spherical cow" joke....We gotta start somewhere.

So, an old hustler maxim is, "You don't know anything until you've played all night". The idea is that that irons out some of the luck. Let's spherical cow it.

We know from the stuff we've already done, that in a race to 8, a slightly better player should win 65.35% of the time. Scaling things up, what happens if the race is to 48?



A little better at 66.51%.

Let's go crazy and race to 160:



Even better at 73.87%.

So far, I've been doing all the work. It's your turn:

In the "let's-play-all-night" scenario, is it more favorable for the better player to play several equal-sized short sets, or one long set?

 

[Bob Callahan]

As someone who has played a lot sports in life, I truly believe there is a such thing as being clutch.

This is what the pros say:

Various baseball analysts, including Bill James, Pete Palmer, Dick Cramer, and the Baseball Prospectus editors, have found so-called "clutch hitting" ability to be a myth. This is not to say that clutch hits, like those listed above, do not exist, but rather that some kind of innate ability for a player to perform above his true talent level in high-pressure situations is nothing but an illusion. In his 1984 Baseball Abstract, James framed the problem with clutch hitting this way: "How is it that a player who possesses the reflexes and the batting stroke and the knowledge and the experience to be a .262 hitter in other circumstances magically becomes a .300 hitter when the game is on the line? How does that happen? What is the process? What are the effects? Until we can answer those questions, I see little point in talking about clutch ability."

From: http://en.wikipedia.org/wiki/Clutch_hitter

 

[Bob Jewett]

For another discussion of probability at billiards, see http://www.sfbilliards.com/articles/1996-06.pdf

Here is a discussion specifically about long runs at 14.1: http://www.sfbilliards.com/articles/2006-06.pdf

 

[Bob Jewett]

Unfortunately our lifetime is too short to get a good statistics in any field.
What you are saying is more related to common sense than statistics, which tries to explain some of the laws behind what we are calling chaos.

Obviously we can never have perfect knowledge, but that is not what probability and statistics is about. The whole point is to be able to make accurate predictions with incomplete knowledge. Statistics gives us the tools to do that and to say how good the predictions are.

 

[Mr441]

.

My son majored in math and works with statistics. He follows sports and analyzes a lot of the data. He claims there is no such thing as a clutch hitter in baseball. It is just something people like to imagine or talk about.

.

Tell that to David Ortiz

 

[pYco]

Obviously we can never have perfect knowledge, but that is not what probability and statistics is about. The whole point is to be able to make accurate predictions with incomplete knowledge. Statistics gives us the tools to do that and to say how good the predictions are.

Yes, you are right. Needless to say though that what we are using now as "tools" to make predictions requires a lot of improvement, otherwise theories like Higgs boson would have been demonstrated long time ago...

 

[Bob Callahan]

Needless to say though that what we are using now as "tools" to make predictions requires a lot of improvement, otherwise theories like Higgs boson would have been demonstrated long time ago...

Oh My! I'm an M-theory guy--but only because one of my friends is a particle guy who works on the Higgs thingie, and it irks him. I'm more of a theoretical math dude than an applied math dude, anyway. I'm interested in extensions of Gödel's stuff, algorithmic information theory, number theory, and the like.

Say, if you are interested in the incompleteness of scientific theories, Jolly Mathen's stuff is a good place to start:

http://www.galilean-library.org/sit...-mathen-incompleteness-and-scientific-the-r43

There'll be a quiz on Tueday.

 

[Bob Callahan]

Tell that to David Ortiz

Never met him. But I have hung out some with Darwin Ortiz.
Wonder if they are related....

 

[pYco]

Oh My! I'm an M-theory guy--but only because one of my friends is a particle guy who works on the Higgs thingie, and it irks him. I'm more of a theoretical math dude than an applied math dude, anyway. I'm interested in extensions of Gödel's stuff, algorithmic information theory, number theory, and the like.

Say, if you are interested in the incompleteness of scientific theories, Jolly Mathen's stuff is a good place to start:

http://www.galilean-library.org/sit...-mathen-incompleteness-and-scientific-the-r43

There'll be a quiz on Tueday.

You don't have to take it personal, my friend. Is not your fault that humanity still have unanswered questions.

 

[jason]

This is what the pros say:



From: http://en.wikipedia.org/wiki/Clutch_hitter

We have adrenaline. We don't run on adrenaline every moment of everyday, only on in certain situations.

All things are not equal. I don't think all athletes are equal under pressure situations. Some players love the big stage. Maybe they are underachievers, but non the less they preform above average in these situations.

Just because one pro says it is not true doesn't make it so. There are probably the same number of pros who will say it is true.

This is something that is extremely difficult to prove if not impossible. Different people will have different opinions, but I stick with my beliefs on this one.

P.S. Remember that clutch hitting is frequently competing against clutch pitching.

 

[Bob Callahan]

We have adrenaline.

There are several interesting ideas in your post, and I am not the kind of person who will argue about someone else's personal experiences. As an athlete, though, since all the things I actively enjoy require precision, clear-mindedness, etc...I try to avoid adrenaline.

There's pretty good evidence supporting me. Here's an abstract of an older paper I found interesting. I've taken the liberty of bolding the parts I found most interesting for pool, and italicizing the part that best seems to support your idea.

In general, the literautre [sic] review provides theoretical explanations for the popular, common-sense belief that a little stress improves performance, whereas when stress becomes severe, performance declines and ultimately breaks down. In terms of psychological stress (as opposed to physiological) the single most important variable appears to be the subject's interpretation of the stress-producing stimuli. Increases in adrenaline and noradrenaline accompany a variety of emotional responses, but differential proportions are not seen as characterizing the various emotions. Noradrenaline secretion appears to be related to physiological stress, or the amount of work attempted by the organism. Adrenaline secretion seems to be more-directly related to mental stress and emotional response. As emotional involvement increases, adrenal medullary secretion of adrenaline increases. The accompanying physiological and metabolic responses faciltate performance to a point; however, extremely high levels of arousal may adversely affect the athlete's proficiency. This is expecially true of sport skills requiring steadiness, precision, and concentration. Finally, for the sake of perspective, it should be stated that any contribution or complication created by the catecholamines is minimal when the entire ability range of competitors is considered. Whereas near superhuman feats by ordinary individuals caught in life-threatening situations have been reported, variations of great magnitude are unlikely in sport. The average individual is not transformed into a world class athlete merely by "getting the adrenaline flowing." Among athletes of similar physical stature and physiological function, however, adrenaline and arousal may certainly tip the scale of performance in sport.

The paper is: Adrenaline, arousal and sport.

People are pretty complicated, and like I sometimes say in my sig, "Our minds are smarter than our science".

I'm a pretty calm guy whether it's pool, karate, or climbing rocks.