Hi Bob, my responses below maked by *
Colin says:
> the SF Billiard Academy theory
Gosh, Colin, you give the SFBA far too much credit. You really need to read some more on billiard physics from authors like Coriolis, Marlow and Koehler. It's important to realize that there are lots more people thinking about these things than you and me.
*I don't assume your work is totally independent, but sure I would like to read more from those sources. I've been trying to get my hands on a copy of Coriolis' Physiques De Je Billiards (sp?) for years. But I don't have a problem with the math Ron has presented, its just a couple of assumptions, and there appears to be a lack of physical evidence to justify these.
> the supporters believe that an off centre hit will produce a force along the normal
> line between the tip contact point and the centre of the cue ball.
Fortunately for all of us, the observed phenomena can all be explained by two conditions: The tip does not slip on the ball during a collision, producing a normal hit, and the tip does slip on the ball if a miscue occurs. Sometimes there are minor miscues, perhaps when the tip starts to slide at the end of contact, but these are still major departures from normal hits.
*But we cannot observe accurately this collision interface. We have to speculate. I think it is reasonable to assume, that in a good contact shot with 'let's say' 5mm to the side of centre, that some fibere and chalk grains will move before effectively locking. Given that we easily accept the idea that when 2 balls collide their is about 2% friction. (I know this is a dubious descriptions, but you'll get what I mean), I don't see why it is so hard to believe that when a cue tip grips, there cannot be 2% slippage.
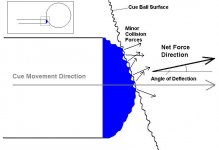
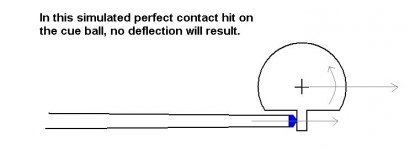
> The diagram below should make this clear. It this collision, there is NO deflection
> . Just spin, with the object travelling in the same line that the cue.
Yes, and a similar diagram is somtimes used when explaining a shot with spin and no slipping. What that explanation overlooks is the movement to the side of the tip that must occur while the tip is on the ball because as the ball starts to rotate, the tip, if it does not slip, must also move to the side.
* Yes, this makes sense. The tip is basically pushing itself in the side via the ball circumference. Is this what you believe is the sole contributary force of deflection?
> In a real tip/ball collision, there are literally millions of tiny collisions at the molecular
> level. All pushing through the norman angle. The properties of the surface interface
> determines where these force directions are.
Well, maybe, but the practical result is that the surface of the tip and the surface of the cue ball do not move aganist each other -- they do not slip.
* Do you have any evidence of this? The videos are inconclusive, and as I said before, minor parts of the tip and chalk will move around exerting forces, many of which we could assume are normal to the collision interface surface.
> The primary factor is creating a tip/ball interface that creates as many force lines
> as possible along the line of the cue.
Sorry, Colin, you can't do any better than the two surfaces not moving against each other. Or are you proposing a tip that actually crawls backwards during the stroke? Even if such a thing could be made, do you really believe it would make the stick more accurate?
*But I believe there is movement. And far more important than this I believe that even where there isn't movement there are forces acting along lines other than the direction of the cue. And given the angle of the tip/ball interface, it is likely there are more forces in a direction toward the centre of the cue ball. Just as there is when two balls collide, but to a lesser degree.
> When we learn how to improve this interface property, we will see some great
> progress in reducing deflection.
This is what Colin believes. I believe that the best you can do is a tip that doesn't slip on the ball. It may be that a better kind of chalk will let you hit without a miscue farther from the center of the ball, and clearly there are bad brands of chalk that miscue where they shouldn't, but I don't expect to see large differences in the near future.
* The key issue here, is if there is an origin of force that acts to increase deflection, as I have postulated, then it must be accorded the staus of a variable in deflection. I still believe there is some slip, and we only need 1% for this to be considered relevant. More importantly, I think the way in which the tip/chalk/cue interface lock determines degree to which linear forces, down the length of the cue are imposed in proportion to forces of the minor surface collisions in other lines.
Colin, increasing the end mass by wrapping lead wire around the ferrule is observed to directly increase the amount of squirt a cue had. So far as I understand your ideas, you have no explanation for this, since it doesn't change the nature of the surfaces.
*I have explained this as I have proposed forces acting to contribute to deflection. Obiously any force pushing against the cue to the side, must be reacted upon by the weight it resists. Hence, a high endmass cue, will increase these forces on the ball, increasing deflection.
Colin, have you tried your ideas on someone who does the physics of friction for a living?
*Uh...do you count?
Are you trying a claim to authority fallacy on me? But heck, introduce me to one if you know one. I ain't scared! I'll go head to head with any Nobel Prize winners in Economics too if you know any
I have some background in material science. That may account somewhat for how I think about what is going on at the micro level.
Could have done without all that physics stuff. Colin, when you write yours, I hope it be such that an ordinary person can understand what you are saying.
