Not really, all you have to for guys like that is ask them a simple question, and 5 years later they'll still be trying to explain their answersYou really went all out on this! I bet it sure rattles some peoples cages!
Great Post!
TFT
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Dreaming of and designing my own pool table
- Thread starter MamboFats
- Start date
Unless you're giving directions to build a frame for a 3C table, you havent accounted for the drop pockets interference with your frame design! Thats the problem when you simply draw something up, you're not accounting for everything that goes into building a pocket pool table, like the slate shelfs and drop pocketsAnd that brings me to today's installment...beams. Beams are very important. If you really understand how beams work, then you can understand pool table frames a lot better.
A beam is any long member that carries a load over an empty space beneath it. In our case, it will be carrying the weight of the slate, the rails, anything that sits on top of it. But beams are everywhere around us, from flooring joists in our houses, to the floor pan of our automobiles, to the bookshelf in our study. I can't give you a comprehensive method to analyze any beam, that would take a college course and probably a lot more math than most of you want to be involved with. But I can give you some tools and ideas that will help you think about this more clearly, and maybe help you decide between different options.
Most beam analysis looks at three properties:
1. How much load can the beam carry in shear?
2. What bending moment can the beam safely carry?
3. How much will the beam deflect under load?
For the most part, I'm going to skip over the first two items, shear and bending moment. That's because I doubt that they'll apply much to pool tables, unless you get a wild idea to build one out of 1/4" by 1/4" furring strips. They are of tremendous importance to an engineer designing a skyscraper or a ship, for example. If a beam doesn't satisfy the first two criteria, it will simply collapse. But how many times have you heard of a pool table breaking in half and dumping the bed slates on the floor, vs. one that simply sagged so much that the balls rolled crooked? As we saw from the leg example, it only took a slim 3/4" stick to (barely) carry the load without breaking but ensuring that deflection was kept within bound required something at least as substantial as a 2x4. So it will be with the horizontal members as well.
Analyzing a beam for shear is usually simple and something that could probably be taught to most high school seniors. For something called a "statically determinate" beam, bending moment isn't much harder, and anyone familiar with algebra could do that. But deflection and analysis of "statically indeterminate" beams requires calculus and is typically taught in about the second year of engineering school. I'm not interested in solving a new calculus problem for every example I want to show you, and unless you want to learn a bunch of math, you're probably not interested in seeing that. Fortunately, we have the magic of the internet to do the heavy (mental) lifting for us.
I'll be using this calculator here (https://clearcalcs.com/freetools/beam-analysis/us) to do the calculations. Go ahead and take a quick look at it, you might find it more convenient to put it in a new tab (right click and select new tab in most browsers).
When you first go to that page, it has a default example. That's a 10' steel beam (I can tell by the Young's Modulus, 29,000,000) sitting on two supports, carrying an evenly distributed load that starts at 100 lbs/foot at the left end and ramps up to 1000 lbs/ft at the right end. I can also tell by looking up in a table that it's a steel I-beam that is 14" tall and weighs 68 lb/ft (680 lbs overall)...far stouter, stronger, and more expensive than anyone in their right mind would use to build a pool table out of, but just the ticket for building a floor in an office building.
As for how it behaves, I can also tell from looking at the right hand side of the page that it carries the most shear load right at the right support, the most bending moment about 5.6' from the left support, and sags 0.00592", just shy of six thousandths, at a point 5.12' from the left support.
All told, a very useful calculator. Now, let me conclude today with a more practical example that illustrates something about what we call "end conditions", or how a beam is attached to something.
First, let me change the beam to a 10x10 carrying an even 1000 lbs/ft, let's say 5 tons of sandbags evenly distributed along its length. Young's modulus will become 1,300,000, I'm going to ignore Area because it doesn't affect the result, "Second moment of inertia" becomes 610. The top part of the left hand side should look like this:
View attachment 632506
And the bottom left side should look like this:
View attachment 632507
On the right hand side, we're interested in this graph:
View attachment 632508
If you mouse over that graph (on the beam calculator page, not on this post), you'll see that maximum deflection is 0.284" at the midpoint of the span, 5' from the left support. So, 5 tons of sandbags would make even a mighty 10x10 sag over 1/4".
An engineer would call this a "simply supported beam", as if it was just lying on two (very strong) sawhorses, spaced 10' apart. Let's look at what happens if I remove one of the sawhorses, and clamp one end of the beam so that it doesn't just fall over.
Change the left support to "fixed", and delete the right support (just click on the trash can symbol to delete it).
View attachment 632509
Now, look at the deflection curve.
View attachment 632510
If you mouse over this graph on the beam calculator page, you'll see that the maximum sag is 2.72"...nearly 10x as much!
In fact, if you shorten the beam to 5':
View attachment 632511
And redistribute the same 5 ton load over 5' instead of 10' (2000 pounds per foot instead of 1000 pounds per foot):
View attachment 632512
You'll see that the deflection is still worse at 5' than at the midpoint of the simply supported span, 0.34" vs 0.284".
View attachment 632513
And that's today's installment. When we dangle something off the edge like that, we call it a cantilever. Cantilevers are all around you as well, from those nifty tables that wheel in over your hospital bed when you're not feeling so well, to this particular house:
View attachment 632515
Now, while it is certainly possible to design a pool table that is completely cantilevered from one end (sounds like a fashion statement!) that plays rock solid, I hope you can appreciate how it is much easier and cheaper to do so with one that is simply supported...you know, with legs at each end.
In the next installment, I hope to show how this might be made even easier with a combination of cantilevers and simple spans.
You can call me if you want, 702-927-5689Thanks, I want it to be unique ... this is to be a one in a lifetime built.
And I'm planning to post all the steps in designing and building in this thread
Regarding the slate screws: do you mean Diamonds don't have the slate screwed down? Only the rail bolts holding it in place?
MamboFats
Active member
thx for the offer, but not the cheapest call from Belgium.You can call me if you want, 702-927-5689
This weekend and next week I'm stopping by at my home club, where 10 new Rasson Magnum II Snooker tables are being assembled. Last week I had a look at the first frame being built with the heating elements. This week they completed the first table, and by now they are up at number 4 or 5. Next, I will be laying on my back under the table to figure out the way they work.
I will be learning a lot from this.
Just play pool ...
Keep in mind, those slates don't mount to the frame, they're free floating.thx for the offer, but not the cheapest call from Belgium.
This weekend and next week I'm stopping by at my home club, where 10 new Rasson Magnum II Snooker tables are being assembled. Last week I had a look at the first frame being built with the heating elements. This week they completed the first table, and by now they are up at number 4 or 5. Next, I will be laying on my back under the table to figure out the way they work.
View attachment 632612View attachment 632613View attachment 632614
I will be learning a lot from this.
Just play pool ...
First, I do want to apologize for the length of my last post. It's just that there were some preliminaries to get out of the way, and I wanted MamboFats to understand how to use a tool in case he had some new idea that he wanted to explore. My examples will get less theoretical and more practical as I go.
I also want to say that I appreciate the contribution of realkingcobra here, probably a lot more than he thinks I do. I've got the theory, and that will get you to the ballpark instead of wandering around some of the less savory parts of town. But he has the practical knowledge and the fine details, and if you want to know just how to lay out the batter's box, I'd refer you to him. I would hope that when we get to areas where I have no firsthand knowledge that we could turn to him to lead us forward.
So last time, I showed that supporting a beam on both ends stiffens it much more than twice as much as supporting it on one end like a diving board, in fact it becomes as much as 9 or 10 times as stiff. This time, I want to play around a little bit with beam lengths and loads, moving loads around to see what effect that has. Along the way, we might learn why most of those big 12-foot snooker tables have 6 legs (or more).
Let me start with the slate from a 7' table resting on a single 4x4. Without looking it up, I'll assume that the slate is 46"x85" and 3/4" thick. If the slate is 2.691 grams/cubic centimeter, that works out to 285 lbs. 85" = 7.083', so that's 285/7.083 = 40.24 lbs/ft.
Our 4x4 is soft pine, so E = 1,190,000 psi. It measures 3.5x3.5" (blame the lumber industry for shorting you a half inch on each side), so I = 12.51 inches^4. We'll support it at each end, so it looks like this:
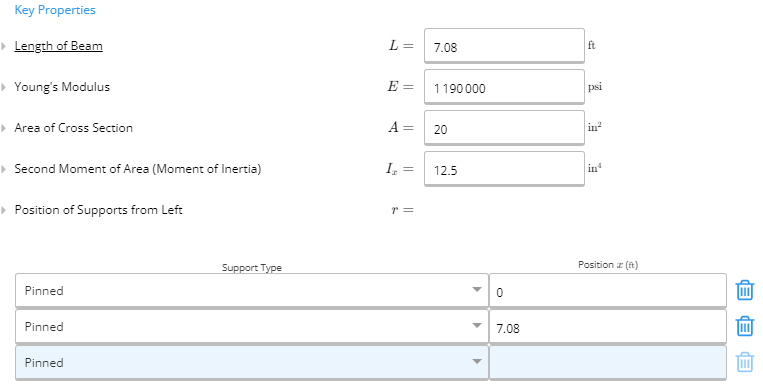
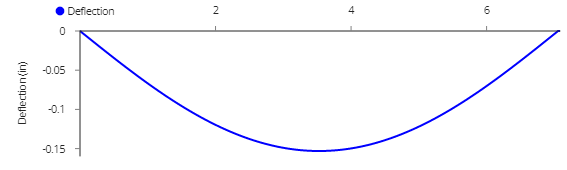
When we go over to the results side and mouse over the deflection graph, we find maximum sag is right in the middle of the beam at 3.54' and measure 0.153"...more than 1/8".
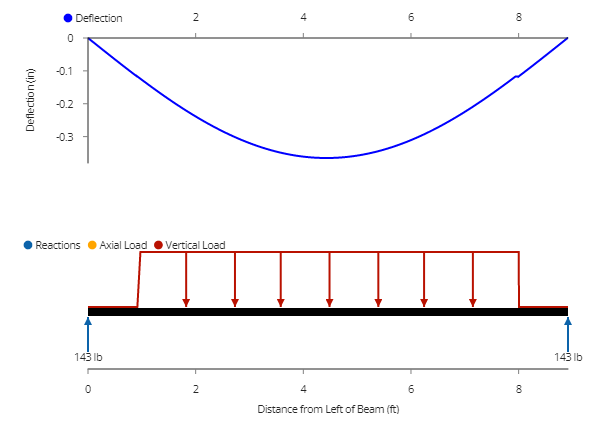
Now, let's say we have a 107" beam left over from some 9' table project, and we're too lazy to cut it down to the correct size. We lay our 7' table on top of it. How much does it sag?
Even though the beam is less than 2' longer, sag is over twice as much at 0.365". And that's with the exact same load as the 7' table, things would be even worse with a 9' slate.
So, important note: all else being equal (and it rarely is), longer beams deflect more. Is there anything we can do to make our beam think that it's shorter than it is?
Let me put that 9' slate on, and then move the legs in a little bit from the very ends. I find that if I move the legs in 1.99' from each end, the sag in the end cantilevers just about matches the sag in the middle. Even though I've now got 66.5 lbs/ft instead of 40.24 lbs/ft, my worst sag has decreased to only 0.0133"...more than 10x less than the same beam with the lighter 7' slate supported at the ends!
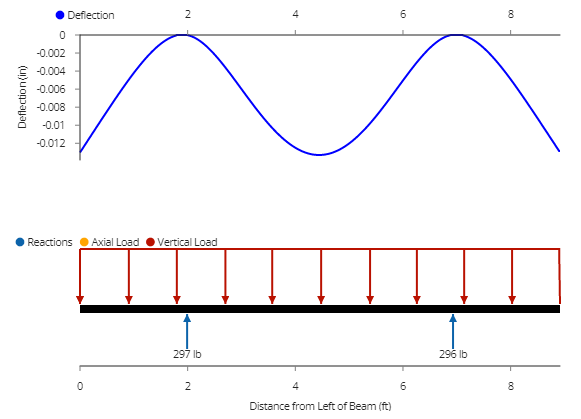
But, I mean, that's crazy! Who would ever build a pool table with the legs set in from each end like that?


Oh. Never mind.
I also want to say that I appreciate the contribution of realkingcobra here, probably a lot more than he thinks I do. I've got the theory, and that will get you to the ballpark instead of wandering around some of the less savory parts of town. But he has the practical knowledge and the fine details, and if you want to know just how to lay out the batter's box, I'd refer you to him. I would hope that when we get to areas where I have no firsthand knowledge that we could turn to him to lead us forward.
So last time, I showed that supporting a beam on both ends stiffens it much more than twice as much as supporting it on one end like a diving board, in fact it becomes as much as 9 or 10 times as stiff. This time, I want to play around a little bit with beam lengths and loads, moving loads around to see what effect that has. Along the way, we might learn why most of those big 12-foot snooker tables have 6 legs (or more).
Let me start with the slate from a 7' table resting on a single 4x4. Without looking it up, I'll assume that the slate is 46"x85" and 3/4" thick. If the slate is 2.691 grams/cubic centimeter, that works out to 285 lbs. 85" = 7.083', so that's 285/7.083 = 40.24 lbs/ft.
Our 4x4 is soft pine, so E = 1,190,000 psi. It measures 3.5x3.5" (blame the lumber industry for shorting you a half inch on each side), so I = 12.51 inches^4. We'll support it at each end, so it looks like this:
When we go over to the results side and mouse over the deflection graph, we find maximum sag is right in the middle of the beam at 3.54' and measure 0.153"...more than 1/8".
Now, let's say we have a 107" beam left over from some 9' table project, and we're too lazy to cut it down to the correct size. We lay our 7' table on top of it. How much does it sag?
Even though the beam is less than 2' longer, sag is over twice as much at 0.365". And that's with the exact same load as the 7' table, things would be even worse with a 9' slate.
So, important note: all else being equal (and it rarely is), longer beams deflect more. Is there anything we can do to make our beam think that it's shorter than it is?
Let me put that 9' slate on, and then move the legs in a little bit from the very ends. I find that if I move the legs in 1.99' from each end, the sag in the end cantilevers just about matches the sag in the middle. Even though I've now got 66.5 lbs/ft instead of 40.24 lbs/ft, my worst sag has decreased to only 0.0133"...more than 10x less than the same beam with the lighter 7' slate supported at the ends!
But, I mean, that's crazy! Who would ever build a pool table with the legs set in from each end like that?
Oh. Never mind.
MamboFats
Active member
No need to apologize, I'm having a blast ...First, I do want to apologize for the length of my last post. It's just that there were some preliminaries to get out of the way, and I wanted MamboFats to understand how to use a tool in case he had some new idea that he wanted to explore. My examples will get less theoretical and more practical as I go
Last year I dove into the calculation of airy points until my head started spinning. I think that was the moment I decided on 6 legs instead of 4: reducing the possibility of sagging beams (no beam is unsupported for longer than ±38").
I like the design of it and I never looked back ...
@El Jefe
I'm looking forward to your contributions on my thread.
I'm planning on starting the build of the legs within a month or 2.
I'm living in Belgium, a small country with limited energy resources of its own: we import processed oil and petrol, gas and a lot of electricity.
The war in Ukraine is pushing a lot of those prices upwards to incredible prices (filling up my car at 6.75€ a gallon, my electricity bill multiplied by more than 2), so the frequency of visiting my local pool venue will be down. So I'm glad on my decision to have my own table in the nearby future.
Stay cool, play pool ...
MamboFats
Active member
This month I finally got to some glueing.
First I pre-drilled all the rubberwood panels for screws to let harden the glue
Thank got for a quality battery powered screwdriver

For 6 legs, I have 24 sides that are a glue up of 28mm of solid oad with 18mm of rubberwood panel
Total 46mm => that is close to 1¾" of thickness
These are really heavy, the base of my table will be overkill

Next step will be routing the slots for the internal horizontal pieces.

I will use an old scratched door thats perfectly flat, for the base of a routing jig.
I will put down 4 sides of 1 leg so I can route each of the 3 slot in one pass over the 4 legpieces
Because of the tapered leg these slot can not be 90°, they have to be angled a little.
First I pre-drilled all the rubberwood panels for screws to let harden the glue
Thank got for a quality battery powered screwdriver
For 6 legs, I have 24 sides that are a glue up of 28mm of solid oad with 18mm of rubberwood panel
Total 46mm => that is close to 1¾" of thickness
These are really heavy, the base of my table will be overkill
Next step will be routing the slots for the internal horizontal pieces.
I will use an old scratched door thats perfectly flat, for the base of a routing jig.
I will put down 4 sides of 1 leg so I can route each of the 3 slot in one pass over the 4 legpieces
Because of the tapered leg these slot can not be 90°, they have to be angled a little.
Last edited:
MamboFats
Active member
The glue up of the 2 panels may nog always be perfectly aligned, but that is of no concern here. The angles to be cut will be in relation to the solid oak, the rubberwood will be cut away at 45° degrees.
So to figure out the angle of the slots to be routed, I took these steps:
1. As you see, the solid oak has a little chamfer on all sides.
This chamfer I want to use in the design. The corners of the assembled legs will not be perfect flush.

2. On the bottom I draw the 45° angles, starting just at the chamfer

3. Same 45° angle on the top side, but now aligning to the outside of the solid oak

4. Now, on the inside of the leg (the rubberwood panel) I can connect the markings and see the taper of the future leg.

5.I also drew a 90° line, so I could measure the angle. This turns out to be not accurate enough.

So I turn to calculating: I know the lenght and I can measure the distance between the 2 lines at the end.
And then I visit : Right Angle Calculator
The answer I get =
Given a=34 and b=425,
∠α = 4.574° = 4°34'26" = 0.07983 rad
I'm not yet sure how to cut these slots:
1. I can use a router, but need a jig to get that angled cut
2. I can use a circlesaw, by angling the blade.
The second option requires multiple passes since the blade is only 4mm thick, the router will need probably only 2 passes with a ¾" flush trim router bit.
For the 2 methods, there will a difference in result, and that is the bottom of the slot. With the router it will be angled as is the complete groove. With the circlesaw there will be a small groove for every pass of the saw. Maybe this is not a bad thing, since this makes for more glue surface.
This project is moving along very slowly, but that's how I like it.
I am not in a rush...
Be happy, play pool
So to figure out the angle of the slots to be routed, I took these steps:
1. As you see, the solid oak has a little chamfer on all sides.
This chamfer I want to use in the design. The corners of the assembled legs will not be perfect flush.
2. On the bottom I draw the 45° angles, starting just at the chamfer
3. Same 45° angle on the top side, but now aligning to the outside of the solid oak
4. Now, on the inside of the leg (the rubberwood panel) I can connect the markings and see the taper of the future leg.
5.I also drew a 90° line, so I could measure the angle. This turns out to be not accurate enough.
So I turn to calculating: I know the lenght and I can measure the distance between the 2 lines at the end.
And then I visit : Right Angle Calculator
The answer I get =
Given a=34 and b=425,
∠α = 4.574° = 4°34'26" = 0.07983 rad
I'm not yet sure how to cut these slots:
1. I can use a router, but need a jig to get that angled cut
2. I can use a circlesaw, by angling the blade.
The second option requires multiple passes since the blade is only 4mm thick, the router will need probably only 2 passes with a ¾" flush trim router bit.
For the 2 methods, there will a difference in result, and that is the bottom of the slot. With the router it will be angled as is the complete groove. With the circlesaw there will be a small groove for every pass of the saw. Maybe this is not a bad thing, since this makes for more glue surface.
This project is moving along very slowly, but that's how I like it.
I am not in a rush...
Be happy, play pool
DeeDeeCues
Well-known member
Contemplation on shims
One the most intriguing things on a regular pooltable are the shims for leveling the slate.
Thinking about it, tells me that a big, heavy slate is only directly supported by a couple of dozens of small wood pieces, totalling maybe 20 square inches of contact between the slate and the frame. This is a lot weight for such a small surface to handle. Although this technique has been used for decades on millions of tables, I find this disturbing.
When looking at the leveling system on a Diamond table: that's a whole other story. Diamond uses 22 wedges, about 10inches long (as I estimate from pictures), where each wedge has a contact surface with the frame of probably 15 square inches or more ... EACH. So the slate is supported by hundreds of square inches ... this, to me, is very reassuring and comforting.
In the final design of my table I will be installing some Diamond inspired leveling system. But, that's not for this post.
Thinking of the shims ... I tried to work out an enhanced version, inspired by Diamond.
Using regulars shims, you squeeze a triangular wedge between two flat parallel surfaces. Obvious, at best, only one surface of the wedge touches one of the other surfaces (bottom of slate or top of frame). The squeezing probably enlarges the contact surface, but never will it fully contact the two sides of the wedge.
I had this idea, maybe it has been before, maybe not, ... but I didn't find anything similar online. I'll share it with you.
These pictures shoud make clear what I'm thinking of:
View attachment 603052
View attachment 603053
View attachment 603054
and here is the side view:
View attachment 603055
View attachment 603056
View attachment 603057
In my design the frame has a cutout, the width and form of the wedge. So, when the wedges makes full contact with the bottom of the slate, the top of the frame makes full contact with the bottom of the wedge. Maximum contact in any case, the weight is distributed over a big surface.
I've covered the wooden wedge with a metal U-casing, for tapping with a hammer, not only on the outside, but also on the inside of the frame. When tapped too far (too high), you can tap it back from the other side to lower the wedge/slate, always in full contact with all surfaces.
I just come to think of making the outside edge of this metal casing a little longer, so it can also function as a stop when contacting the frame.
The angle of the wedge and it's length make for the maximum height adjustment. When playing with angle and dimensions you can alter the maximum height that can be achieved.
When applying shims, I've noticed a lot of mechanics placing two shims close together, left and right from a slate screw (makes sense to me). So I slotted my wooden/metal wedge so it can be placed right under the hole for the slate screw, with the slate screw going through the wedge - not obstructing - into the frame (of course, longer screws needed).
Since I use the name Desain Design for my blog and website, I'm calling this DSLS - Desain Slate Leveling System.
If anyone ever wants to use this design commecially, contact me ...
I'm dreaming, right ...
I am looking for maximum weight support all along the complete design of my table, from top to bottom.
A lot of pool tables have adjustable feet, which is only a threaded rod (3/4" of so). This is IMO the next weak point in the weight distribution. But that's is for another post.
I love to hear from you ... thoughts, ideas, I'm open to your criticism.
Your calculation results in about 30psi for the shims. That is nothing. You can press harder with your thumb.
Call collectthx for the offer, but not the cheapest call from Belgium.
This weekend and next week I'm stopping by at my home club, where 10 new Rasson Magnum II Snooker tables are being assembled. Last week I had a look at the first frame being built with the heating elements. This week they completed the first table, and by now they are up at number 4 or 5. Next, I will be laying on my back under the table to figure out the way they work.
View attachment 632612View attachment 632613View attachment 632614
I will be learning a lot from this.
Just play pool ...
MamboFats
Active member
Question for the experienced wood workers.
I'll use my circular saw with a diy track saw guide for cutting the taper.
I can choose cutting the 45°angle, cut-off is on the 135° side of the blade
or cutting the 135°, with the cut-off on the 45° side of the blade
Any suggestions?
I think cutting 135° is favorable, but love to hear any comments or other suggestions.
thx
I'll use my circular saw with a diy track saw guide for cutting the taper.
I can choose cutting the 45°angle, cut-off is on the 135° side of the blade
or cutting the 135°, with the cut-off on the 45° side of the blade
Any suggestions?
I think cutting 135° is favorable, but love to hear any comments or other suggestions.
thx
Careful... Based on all the theory your thread has collected. You may not want to go down the hole of what and how to make something that actually "perfectly flat"...lolI will use an old scratched door thats perfectly flat, for the base of a routing jig.
Love your build by the way.
I only really pay attention to two things when setting up for cuts of any kind.Question for the experienced wood workers.
I'll use my circular saw with a diy track saw guide for cutting the taper.
I can choose cutting the 45°angle, cut-off is on the 135° side of the blade
or cutting the 135°, with the cut-off on the 45° side of the blade
Any suggestions?
I think cutting 135° is favorable, but love to hear any comments or other suggestions.
thx
- Most rigid set up as possible to help control deviation
- Guides, references or whatever are used to prevent deviations from altering the work piece. Off cuts are general sacrificial.
DeeDeeCues
Well-known member
Everything you just mentioned is nothing but word salad!
Explain why the 6 leg 1912 Regina 10' billiards table i set up in Billings, MT had almost NO weight on the center legs!
Slates were 1 1/2" thick.
Because you screwed up?
MamboFats
Active member
to all gentle(wo)men on this forum, reading posts in my topic.
I appreciate posts of an educational nature, may be critisizing, may be supporting.
Even a little off topic, I don't mind, as long as we get back on track.
But I already know how to swear, how to curse and how to push people down... I don't like that and this is not the place
This is a place for all who love the game of pool
Please respect my thread
thank you
I appreciate posts of an educational nature, may be critisizing, may be supporting.
Even a little off topic, I don't mind, as long as we get back on track.
But I already know how to swear, how to curse and how to push people down... I don't like that and this is not the place
This is a place for all who love the game of pool
Please respect my thread
thank you
MamboFats
Active member
So last night I put some supports under my spare door and today I started preparations for cutting the slots
1. some pieces of wood aligned for the exact width of the legpieces

2. for a total of 4 legpieces = 1 complete leg to be handled in one pass

3. some not-perfect cuts will be dealt with in this jig.
those leg pieces fit really snug and are not moving. I can always use some double sided tape to secure them even more

Drilling and using the jigsaw is no problem since the noise these machines make is not really loud. Using my circular saw is something else: she screams and yells for everyone to hear.
My house is between 2 other and for the next 10 days I won't be home before late at night. I try to respect my neighbors and keep it quiet after 19h00. My first day off will be saturday, june 4th. Hope to have time.
Enjoy pool...
1. some pieces of wood aligned for the exact width of the legpieces
2. for a total of 4 legpieces = 1 complete leg to be handled in one pass
3. some not-perfect cuts will be dealt with in this jig.
those leg pieces fit really snug and are not moving. I can always use some double sided tape to secure them even more
Drilling and using the jigsaw is no problem since the noise these machines make is not really loud. Using my circular saw is something else: she screams and yells for everyone to hear.
My house is between 2 other and for the next 10 days I won't be home before late at night. I try to respect my neighbors and keep it quiet after 19h00. My first day off will be saturday, june 4th. Hope to have time.
Enjoy pool...
Attachments
This could be my final design.
Since I'm on a real quest, searching for the best (???), I have it in my head that a 4-legged table can be topped by a 6-legged table.
6 legged tables are just cool period.
I think a 2 inch slate would weigh about 400 pounds
A 400 pound slate sounds fun! Especially on stairs.
MamboFats
Active member
I'm exhausted, just want to put this up before taking a shower and enjoying an evening with drinks and appetizers.
Today, I had the opportunity to use a professional setup at a carpenter's workplace.
It started with him suggesting to use his glue clamping equipment. So, I did

I've got my 10' long oak and rubberwood glued and clamped. They will stay like this for 24 hours.
And while I was there, I got to use his big panel saw.
A few posts ago I was preparing for making the slots in the leg pieces. I did them on a table saw.
With only a 20min lunch break, I was sawing from 10h00 till 15h00.
So, I'm exhausted.
This is the end result: 24 labeled leg pieces, leg 1 to 6, pieces A to D

I grouped the leg pieces, so for each leg all cuts and slots are equal.

All ends and slots are angled to 4.5° what will be the angle of the tapered legs.

This just got serious. I'm way ahead of any schedule I did not have in mind ;-)
Tomorrow at noon I will be enjoying some 3cushion at the club. In the evening I'll be playing some one pocket in my friends mancave.
enjoy pool, enjoy life
Today, I had the opportunity to use a professional setup at a carpenter's workplace.
It started with him suggesting to use his glue clamping equipment. So, I did
I've got my 10' long oak and rubberwood glued and clamped. They will stay like this for 24 hours.
And while I was there, I got to use his big panel saw.
A few posts ago I was preparing for making the slots in the leg pieces. I did them on a table saw.
With only a 20min lunch break, I was sawing from 10h00 till 15h00.
So, I'm exhausted.
This is the end result: 24 labeled leg pieces, leg 1 to 6, pieces A to D
I grouped the leg pieces, so for each leg all cuts and slots are equal.
All ends and slots are angled to 4.5° what will be the angle of the tapered legs.
This just got serious. I'm way ahead of any schedule I did not have in mind ;-)
Tomorrow at noon I will be enjoying some 3cushion at the club. In the evening I'll be playing some one pocket in my friends mancave.
enjoy pool, enjoy life
I hope everything is going ok.
