128 person bar table tournament $$$

JoeyA

JoeyA

Efren's Mini-Tourn BACKER
Silver Member
128 person bar table 9 BALL tournament $$$

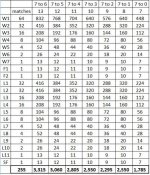
I estimate that in a DE tournament, racing to 7 on both sides there are 190 matches total. I estimate average number of games played per match is 12 games. If the cost of the table is $1 per game, the total coins in the table come to $2280.00. If the event has a $40 entry fee with a full field the purse money would be $5120.00.

I'm not factoring in added money, just looking at total expenses for 128 players.

Do you think these numbers are fairly accurate? If not what are your estimates?
 
Last edited:
JoeyA said:
I estimate that in a DE tournament, racing to 7 on both sides there are 190 matches total. I estimate average number of games played per match is 12 games. If the cost of the table is $1 per game, the total coins in the table come to $2280.00. If the event has a $40 entry fee with a full field the purse money would be $5120.00.

I'm not factoring in added money, just looking at total expenses for 128 players.

Do you think these numbers are fairly accurate? If not what are your estimates?
Click to expand...

Joey,
Your numbers are incorrect. Considering a double set final there will be 255 total matches. If each and every match goes 7-6 there will be 3,315 games played. At $1 / gm that would equal $3,315. At 7-0 there will be 1,785 games played. The answer is somewhere in the middle. If I was to take a guess on average the matches will go 7-4 or 7-5. Somewhere in that range.
 

Attachments

  • games played 128.jpg
    games played 128.jpg
    86.6 KB · Views: 733
Last edited:
You may also apply the percentages of the match occurrences with the anticipated payout sums and take the sum of the average products.

Add a few monte carlo simulations just to be safe.
 
With a standard double-elimination format, the total number of matches for a tournament with N players is 2N-2.

If the final match is true double elimination and it goes to a second set, and you want to count that second set as another match, then the total is 2N-1.

So, the total number of matches would be as follows (add one to each if the finals goes two sets):

4 players = 6 matches
8 players = 14 matches
16 players = 30 matches
32 players = 62 matches
64 players = 126 matches
128 players = 254 matches
256 players = 510 matches
 
Hungarian said:
Joey,
Your numbers are incorrect. Considering a double set final there will be 255 total matches. If each and every match goes 7-6 there will be 3,315 games played. At $1 / gm that would equal $3,315. At 7-0 there will be 1,785 games played. The answer is somewhere in the middle. If I was to take a guess on average the matches will go 7-4 or 7-5. Somewhere in that range.
Click to expand...

Excellent. Just what I was looking for.
Thank you.

tommyceilings said:
Isn't 7-4 or 7-5 a 12 game average?
Click to expand...
The chart Hungarian provided is perfect for my needs as it covers a large group of possibilities.

AtLarge said:
With a standard double-elimination format, the total number of matches for a tournament with N players is 2N-2.

If the final match is true double elimination and it goes to a second set, and you want to count that second set as another match, then the total is 2N-1.

So, the total number of matches would be as follows (add one to each if the finals goes two sets):

4 players = 6 matches
8 players = 14 matches
16 players = 30 matches
32 players = 62 matches
64 players = 126 matches
128 players = 254 matches
256 players = 510 matches
Click to expand...

Thanks!
 
Hungarian,
I went back over my notes and now realize why my count was so far off. Thank you again for the chart.

Joey
 
Monte Carlo references, algebraic formulas. I didn't know so many engineers played pool!:D
 
Diamond69 said:
Monte Carlo references, algebraic formulas. I didn't know so many engineers played pool!:D
Click to expand...

This forum has people who can tell you how to build a rocket ship or show you how to try and tear apart a person's dreams. :p
 
JoeyA said:
This forum has people who can tell you how to build a rocket ship or show you how to try and tear apart a person's dreams. :p
Click to expand...


What ever you need. We can accomodate. You want some math...we got it....you want some clowning...we got it....and you want some trolling....we got it
EDIT: So really the event you describe in your OP will take in somewhere around $2.5 to 3K in quarters. Right?
 
Last edited:
JoeyA said:
Hungarian,
I went back over my notes and now realize why my count was so far off. Thank you again for the chart.

Joey
Click to expand...

Although your numbers were off, you are on to something. I used to do a similar thing with table time (Loser paid and winner moved on, there were no entry fees) I did this for years and had waiting lists for the tournament every week, not to mention they were my best days dollar wise. I turned what were dead Sundays into my best days.
 
macguy said:
Although your numbers were off, you are on to something. I used to do a similar thing with table time (Loser paid and winner moved on, there were no entry fees) I did this for years and had waiting lists for the tournament every week, not to mention they were my best days dollar wise. I turned what were dead Sundays into my best days.
Click to expand...

Like, like.
 
I am guessing the 11 - 15 balls are being removed?

If not...You have to factor in the "save a buck" rack when the opponent rakes the last three balls and they use those pluse the 10 - 15 balls.
 
BRKNRUN said:
I am guessing the 11 - 15 balls are being removed?

If not...You have to factor in the "save a buck" rack when the opponent rakes the last three balls and they use those pluse the 10 - 15 balls.
Click to expand...

VERY GOOD POINT. One of those common sense things that the scientific community here missed. Kind of like lowering the air pressure to get under the bridge.

Prolly need to hit the final number with a .8 if using all 15 balls
 
AtLarge said:
With a standard double-elimination format, the total number of matches for a tournament with N players is 2N-2.

If the final match is true double elimination and it goes to a second set, and you want to count that second set as another match, then the total is 2N-1.

So, the total number of matches would be as follows (add one to each if the finals goes two sets):

4 players = 6 matches
8 players = 14 matches
16 players = 30 matches
32 players = 62 matches
64 players = 126 matches
128 players = 254 matches
256 players = 510 matches
Click to expand...

Simple and to the point.

Thanks,

JC
 
I analyzed the 2011 Western BCA 9 ball tournament open A bracket for you Joey since CSI has all the information there to view and it was a race to 7 event. There were 108 entrants which would predict 214 matches but in actuality there were only 201 matches due to forfeits. This is about 6% which you must take into account since these matches drop no coins in the tables. This is probably about average too. People don't show up at the table in pool tournaments for various reasons.

The losers average score was 3.726 games. Which would mean 10.726 games played per match on average. This was played on Diamond bar boxes.

Easy to calculate entry money depending on the fee. At $1 a game the coins would total $2156 for this event. This does not take into acount practice games which I have no idea how to predict. We paid a $20 green fee which brought in, oddly 108 players times 20 or $2160. Weird eh? But practice was free. IMO the green fee should have been $25 to be fair to the table venders.

Hope this helps,

JC
 
Last edited:
JC said:
I analyzed the 2011 Western BCA 9 ball tournament open A bracket for you Joey since CSI has all the information there to view and it was a race to 7 event. There were 108 entrants which would predict 214 matches but in actuality there were only 201 matches due to forfeits. This is about 6% which you must take into account since these matches drop no coins in the tables. This is probably about average too. People don't show up at the table in pool tournaments for various reasons.

The losers average score was 3.726 games. Which would mean 10.726 games played per match on average. This was played on Diamond bar boxes.

Easy to calculate entry money depending on the fee. At $1 a game the coins would total $2156 for this event. This does not take into acount practice games which I have no idea how to predict. We paid a $20 green fee which brought in, oddly 108 players times 20 or $2160. Weird eh? But practice was free. IMO the green fee should have been $25 to be fair to the table venders.

Hope this helps,

JC
Click to expand...

Excellent analysis. Many things to consider...

thanks,
JoeyA
 
You must log in or register to reply here.
Back
Top