My original post (further below) had overlooked some things and was incorrect. So here is the improved formula and reasoning as seen in post #20 of this thread.
D = Distance from CB to OB (or target) in feet.
V = Velocity Factor where 0 is maximum speed and 4 is slow, or one table length roll including bouncing off one rail.
PPe* is the pivot point required for a 5 foot shot at speed factor 3, which is medium slow, enough to bounce 2 rails back to the original position.
This figure will be different for each cue on each table. It brings the slickness variable into the formula.
My prefered cue on my table has PPe* 13.7 inches. (This could change with humidity changes). It's PPi is 9.5 inches, so my K value for my cue on my table at the moment is (13.7 - 9.5)/15 = approx 0.28.
0.28 is the adjustment needed at distance 1 foot and speed factor 1.
The number 15 is derived from the PPe* being at 5 foot at speed factor 3. 5x3 = 15.
PPe* could use any shot as a basis with a different numerator, but 5 foot is a good number because it is about the length of the cue, it can be played with little elevation and it is long and slow enough to provide a decent difference with PPi, hence giving it a reasonable margin of error. PPe* can vary by around 2 inches depending on cloth slickness. It is a number that can be derived pretty accurately within half a dozen hits on a new table.
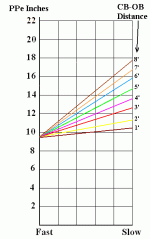
So for any shot my PPe = 9.5 + D x V x 0.28
So if I have a shot at speed factor 2 over 4 feet my PPe = 9.5 + 2.24 = approx 11.7 inches.
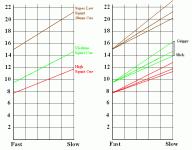
Below is a chart with PPe's for the full range of speeds and distances for my cue. You should be able to plug data into this formula and get PPe's that correspond to those in the chart.
Note: The key to making this formula simple was creating the methodology of the speed factor. In the chart below, the speeds are divided into 6 markings, rather than the 5 for speed factors 0-4, so I will need to redo the graphics and make some clearer statements and do some measurements regarding defining the speeds in a way that others can immitate.
General Speed Factor Rules are:
0 = Max speed, would bounce about 5 rails.
1 = Firm speed, would bounce 4 rails and back to starting position.
2 = Medium speed, would bounce 3 rails and back to starting position.
3 = Slow-Medium speed, would bounce 2 rails and back to starting position.
4 = Slow speed, would bounce 1 rail and back to starting position at center table.
I would appreciate if some people would trial this formula on the table with their own cues and give some feedback, or make any suggestions as to improving the nature of this equation.
Note: This is not a formula based on the physics of swerve, squirt, friction and the likes, it is an equation that roughly imitates the data produced in experiments.
Here is the Effective Pivot Point Equation - 14 Oct 2008
PPe = PPi + [(D-V) x K]
Where K = PPe*/10
Note that (D-V) has a minimum value of zero.
PPe* = The measured effective pivot point for a shot over 5 feet length hit at speed 2. Where speed 2 is approximately the speed required to hit the CB 2 rails and back to its starting position. A relatively slow shot. On my own cue and table PPe* is just under 14 inches.
PPi = The Intrinsic Pivot Point. Estimated by finding the effective pivot point for a shot over 5 feet hitting at maximum velocity, such that swerve has insignificant influence on the shot. My cue's PPi is 9.5 inches. Low squirt cues are 12 to 14 inches.
D = Distance in feet between CB and OB.
V = Velocity Factor, such that 1 travels one table length including 1 bounce of a rail, 2 = 2 table lengths including 2 rail bounces. etc. 5 represents a near maximum power shot.
PPe tells you the required effective pivot point for any shot after you enter the distance and expected shot velocity.
K provides the equation with a factor that takes into account the slickness of the cloth. Each time you play on a different table, you'd need to establish a new K value. A sticky table will have higher K values. Also, low squirt cues will have higher K values. For my table and cue the K value is about 1.5, which means at the lowest speed I need to extend my pivot point 1.5 inches for every foot of extra distance and I reduce the pivot point by 1.5 inches for every number up the velocity scale I increase the shot.
I hope those who use a little BHE will find this equation useful.
Any questions or suggestions?
Please no suggestions telling me to stop thinking so much. Please respect that getting this equation to where it is has taken a lot of thinking, reading, arguing and testing over the years. So if you're not interested, just keep on walking and avoid the thread please.
Colin
PPe = PPi + DVK
D = Distance from CB to OB (or target) in feet.
V = Velocity Factor where 0 is maximum speed and 4 is slow, or one table length roll including bouncing off one rail.
K = (PPe* - PPi)/15
PPe* is the pivot point required for a 5 foot shot at speed factor 3, which is medium slow, enough to bounce 2 rails back to the original position.
This figure will be different for each cue on each table. It brings the slickness variable into the formula.
My prefered cue on my table has PPe* 13.7 inches. (This could change with humidity changes). It's PPi is 9.5 inches, so my K value for my cue on my table at the moment is (13.7 - 9.5)/15 = approx 0.28.
0.28 is the adjustment needed at distance 1 foot and speed factor 1.
The number 15 is derived from the PPe* being at 5 foot at speed factor 3. 5x3 = 15.
PPe* could use any shot as a basis with a different numerator, but 5 foot is a good number because it is about the length of the cue, it can be played with little elevation and it is long and slow enough to provide a decent difference with PPi, hence giving it a reasonable margin of error. PPe* can vary by around 2 inches depending on cloth slickness. It is a number that can be derived pretty accurately within half a dozen hits on a new table.
So for any shot my PPe = 9.5 + D x V x 0.28
So if I have a shot at speed factor 2 over 4 feet my PPe = 9.5 + 2.24 = approx 11.7 inches.
Below is a chart with PPe's for the full range of speeds and distances for my cue. You should be able to plug data into this formula and get PPe's that correspond to those in the chart.
Note: The key to making this formula simple was creating the methodology of the speed factor. In the chart below, the speeds are divided into 6 markings, rather than the 5 for speed factors 0-4, so I will need to redo the graphics and make some clearer statements and do some measurements regarding defining the speeds in a way that others can immitate.
General Speed Factor Rules are:
0 = Max speed, would bounce about 5 rails.
1 = Firm speed, would bounce 4 rails and back to starting position.
2 = Medium speed, would bounce 3 rails and back to starting position.
3 = Slow-Medium speed, would bounce 2 rails and back to starting position.
4 = Slow speed, would bounce 1 rail and back to starting position at center table.
----------------------------------------------------------------------
Original Post
Following on from some other discussions regarding finding the required pivot point, for Back Hand English, which takes into account swerve, I did some further testing today and fiddled around with equations until I got something which I think is a pretty accurate guide for various cues and cloth conditions.Original Post
I would appreciate if some people would trial this formula on the table with their own cues and give some feedback, or make any suggestions as to improving the nature of this equation.
Note: This is not a formula based on the physics of swerve, squirt, friction and the likes, it is an equation that roughly imitates the data produced in experiments.
Here is the Effective Pivot Point Equation - 14 Oct 2008
PPe = PPi + [(D-V) x K]
Where K = PPe*/10
Note that (D-V) has a minimum value of zero.
PPe* = The measured effective pivot point for a shot over 5 feet length hit at speed 2. Where speed 2 is approximately the speed required to hit the CB 2 rails and back to its starting position. A relatively slow shot. On my own cue and table PPe* is just under 14 inches.
PPi = The Intrinsic Pivot Point. Estimated by finding the effective pivot point for a shot over 5 feet hitting at maximum velocity, such that swerve has insignificant influence on the shot. My cue's PPi is 9.5 inches. Low squirt cues are 12 to 14 inches.
D = Distance in feet between CB and OB.
V = Velocity Factor, such that 1 travels one table length including 1 bounce of a rail, 2 = 2 table lengths including 2 rail bounces. etc. 5 represents a near maximum power shot.
PPe tells you the required effective pivot point for any shot after you enter the distance and expected shot velocity.
K provides the equation with a factor that takes into account the slickness of the cloth. Each time you play on a different table, you'd need to establish a new K value. A sticky table will have higher K values. Also, low squirt cues will have higher K values. For my table and cue the K value is about 1.5, which means at the lowest speed I need to extend my pivot point 1.5 inches for every foot of extra distance and I reduce the pivot point by 1.5 inches for every number up the velocity scale I increase the shot.
I hope those who use a little BHE will find this equation useful.
Any questions or suggestions?
Please no suggestions telling me to stop thinking so much. Please respect that getting this equation to where it is has taken a lot of thinking, reading, arguing and testing over the years. So if you're not interested, just keep on walking and avoid the thread please.
Colin
Last edited: