effect bottom has on an object ball when cutting?

[Colin Colenso]

The effect was close to equal, in my measurement. This is also what theory predicts, pretty closely.

And the magnitude?

From what I can understand of the theory, the magnitude of throw decrease would be less than half of the decrease we get from playing the same shot at higher speeds.

 

[AuntyDan]

And the magnitude?

From what I can understand of the theory, the magnitude of throw decrease would be less than half of the decrease we get from playing the same shot at higher speeds.

When you hit a ball hard the main the cue ball will have no spin at the moment of impact, unless it is a very long shot. If hitting with either top or bottom spin will decrease throw compared to a non-spinning ball, then wouldn't the the inverse be that a non-spinning ball throws more, relative to a shot with just natural roll? (Which is the same as top spin.)

Therefore shouldn't hitting hard ought result in more throw, not less? Or does the speed of the cue ball at impact have an effect on throw of it's own regardless of spin?

And talking of spin, I'm getting dizzy and need to go lie down after reading this stuff.

 

[Colin Colenso]

When you hit a ball hard the main the cue ball will have no spin at the moment of impact, unless it is a very long shot. If hitting with either top or bottom spin will decrease throw compared to a non-spinning ball, then wouldn't the the inverse be that a non-spinning ball throws more, relative to a shot with just natural roll? (Which is the same as top spin.)

Therefore shouldn't hitting hard ought result in more throw, not less? Or does the speed of the cue ball at impact have an effect on throw of it's own regardless of spin?

And talking of spin, I'm getting dizzy and need to go lie down after reading this stuff.

Hi Dan,
Tests and theories have indicated that higher speeds do reduce throw significantly.

Below is a graphic of the theoretical predictions and some actual tests.

The reason I raised this is that, I think any compensation required for bottom or top is significantly less than what is needed for speed, and yet most players don't compensate for speed, at least not consciously.

 

[AuntyDan]

Hi Dan,
Tests and theories have indicated that higher speeds do reduce throw significantly.

Below is a graphic of the theoretical predictions and some actual tests.

The reason I raised this is that, I think any compensation required for bottom or top is significantly less than what is needed for speed, and yet most players don't compensate for speed, at least not consciously.

Thanks Colin. This may be strarting to make some sense to me. I have been assuming it is the draw that is causing the extra throw/over cutting of the shots, but now I think about it I usually always hit a draw shot at a medium/slow speed. So the extra throw I am seeing is the result of speed rather than spin?

 

[Jaden]

The harder you hit it the faster it accelerates and the more force behind the contact, therefore, the less spin will have an effect due to the increased force......

Now I don't think that it is the draw necesarily causing the deviation, and the reason that draw appears to affect it more than follow is simple.

When most people draw they either have to or just happen to have their butt elevated and are NOT stroking as straight through the ball as possible.

Where as with follow, they tend to elevate their bridge and stroke straight through the ball. This helps to eliminate swerve for slightly off center shots. No shot will be perfectly on the center line of the CB although the offset may be negligable.

 

[Bob Jewett]

... higher speeds do reduce throw significantly.
...

More precisely stated, the faster the relative speeds between the two surfaces, the lower is the coefficient of friction. This is a general result from materials engineering (so I'm told) and the effect was measured by Wayland Marlow for pool balls and published in his book "Physics of Pocket Billiards."

Using Marlow's measurements, Dave Alciatore calculated curves of throw vs. speed and angle that look a lot like my measurements. I think Dave's graph that is above is an early result that does not take "end of slipping" into account. It turns out that for small to moderate amounts of spin, the balls may get to a state during contact where the two surfaces are moving at the same speed (you might say in lock step) and there is no additional throw.

 

[Bob Jewett]

And the magnitude?

From what I can understand of the theory, the magnitude of throw decrease would be less than half of the decrease we get from playing the same shot at higher speeds.

For a half-ball hit and the balls I was using, the difference was about 3 degrees. I was using a speed that drove the object ball a total of about 2.4 table lengths.

 

[Colin Colenso]

More precisely stated, the faster the relative speeds between the two surfaces, the lower is the coefficient of friction. This is a general result from materials engineering (so I'm told) and the effect was measured by Wayland Marlow for pool balls and published in his book "Physics of Pocket Billiards."

Using Marlow's measurements, Dave Alciatore calculated curves of throw vs. speed and angle that look a lot like my measurements. I think Dave's graph that is above is an early result that does not take "end of slipping" into account. It turns out that for small to moderate amounts of spin, the balls may get to a state during contact where the two surfaces are moving at the same speed (you might say in lock step) and there is no additional throw.

Thanks for that explanation Bob!

 

[Colin Colenso]

For a half-ball hit and the balls I was using, the difference was about 3 degrees. I was using a speed that drove the object ball a total of about 2.4 table lengths.

Do you mean 3 degrees difference between stun v draw at the same speed?

This is considerably higher than I would have guessed. I would have guessed about 1 degree difference at medium (say 10mph) speed.

 

[bustinbob_99]

I also miss this shot more often when using draw. I believe that the reason is that there is so much less room for error.
Oh, if I could only consistantly hit the cue where I intend to!!!!

 

[sixpack]

I also miss this shot more often when using draw. I believe that the reason is that there is so much less room for error.
Oh, if I could only consistantly hit the cue where I intend to!!!!

My old coach and stakehorse told me when I was first learning that you need to be extra careful shooting into the corner pockets with draw. It puts some extra overspin on the OB and make it more likely for the pocket to reject.

I was watching the finals from the challenge of champions (1997) yesterday with Fong Pang Chao and Oliver Ortman, Fong plays a shot down the rail with draw, it hits the pocket in the face and it jars and stays up. If he had hit it without draw, I think it would have fallen in.

Cheers,
RC

 

[Bob Jewett]

Do you mean 3 degrees difference between stun v draw at the same speed?

This is considerably higher than I would have guessed. I would have guessed about 1 degree difference at medium (say 10mph) speed.

Yes, the difference was between stun and draw for a half-ball hit. Follow gave the same angle as draw. The actual measurement was 4 inches in 76 inches of travel.

The difference is larger that I expected also, and I was amazed that draw and follow changed throw the same way, even though that was the prediction from theory.

I think that the speed for the ball going two lengths plus back out to the side pocket is less than 10MPH. I get about 3MPH on a 100-speed table.

 

[Bob Jewett]

I also miss this shot more often when using draw. I believe that the reason is that there is so much less room for error.

I think that the main problem is that if you're going to draw the ball, you nearly always have to hit it harder than for follow shots, and it's the speed that makes the pocket shrink.

 

[Colin Colenso]

Yes, the difference was between stun and draw for a half-ball hit. Follow gave the same angle as draw. The actual measurement was 4 inches in 76 inches of travel.

The difference is larger that I expected also, and I was amazed that draw and follow changed throw the same way, even though that was the prediction from theory.

I think that the speed for the ball going two lengths plus back out to the side pocket is less than 10MPH. I get about 3MPH on a 100-speed table.

I repeated your test and got basically the same results as seen in diagram below.

I banked the OB up and down the table for ease of recording and to expand the variation.

What really spun me out was when I tried it using IE with BHE and got the same path as with bottom spin. This alone proves the significance of reducing friction with increased relative speed and particularly the speed associated with rotation which seems to be more significant than linear speed.

Also, playing center at very high speed still had a bit more throw than a soft bottom spin shot, which also surprised me.

This has completely altered my thinking on BHE systems and their implementation regarding OE and IE and speed.

btw1: The difference bewteen top and bottom was about 1" on average, but it may be due to the difficulty in getting follow on the CB from 2" away from OB.

bwt2: Other variations could occur through accidentally applying a touch of english.

Note, the points on the right are the data I collected, the lines indicate points to the mean.

 

[enzo]

More precisely stated, the faster the relative speeds between the two surfaces, the lower is the coefficient of friction. This is a general result from materials engineering (so I'm told) and the effect was measured by Wayland Marlow for pool balls and published in his book "Physics of Pocket Billiards."

Using Marlow's measurements, Dave Alciatore calculated curves of throw vs. speed and angle that look a lot like my measurements. I think Dave's graph that is above is an early result that does not take "end of slipping" into account. It turns out that for small to moderate amounts of spin, the balls may get to a state during contact where the two surfaces are moving at the same speed (you might say in lock step) and there is no additional throw.

i totally agree with the above because on a pool table it is assuredly the case. there are a lot of cuts you simply can't make with a slow speed becasue the contact point gets out of reach, whereas you can make them with a firm speed.

anyway, the reason for my post. there is a nice diagram in freddies bank book that shows how the surface area of contact increases with speed. my point is, more surface area in contact should translate to increased friction, and thus increased throw. i wonder why that is not the case. i guess the effects of slow speed just overshadow and effects of increased contact area.

 

[Colin Colenso]

there is a nice diagram in freddies bank book that shows how the surface area of contact increases with speed. my point is, more surface area in contact should translate to increased friction, and thus increased throw. i wonder why that is not the case. i guess the effects of slow speed just overshadow and effects of increased contact area.

The larger surface area may in fact be the reason, or part of the reason for reduced throw or a proportional decrease in friction.

eg. Try pushing a table that stands on 4 pointed legs, and then try pushing a table that has a flat bottom. The larger surface area often has less friction. But it's not an absolute rule, it all depends on the surface properties involved.

Another reason could be that as speed and force increases, that the elastic linear forces keep increasing in proportion, while the frictional forces increase more gradually. Hence the net vector is more in line with the linear path through the center of the 2 balls.

 

[Bob Jewett]

...
I think that the speed for the ball going two lengths plus back out to the side pocket is less than 10MPH. I get about 3MPH on a 100-speed table.

On prompting from JAL, I redid my calculations and got about 6.6MPH for the initial speed of the object ball. This depends on how much energy you figure is lost on each bounce on the cushions. I figure about 75% on each bounce, part of which is due to reversal of the spin.

 

[Bob Jewett]

... my point is, more surface area in contact should translate to increased friction, and thus increased throw. ...

The force that causes throw is due to the contact force (or normal force, the balls pushing against each other) and the coefficient of friction for the surfaces of the two balls. Simple theory says that the force of friction is independent of the surface area involved. In fact, it says that the tangential force of friction is just the product of the coefficient and the normal force. I think there is some reduction of the coefficient of friction with higher pressures between the surfaces, but I don't know the details or if any measurements have been done for cast phenolic.

 

[Jal]

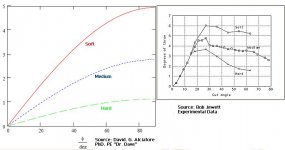
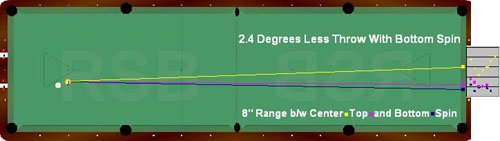
... my point is, more surface area in contact should translate to increased friction, and thus increased throw. i wonder why that is not the case. i guess the effects of slow speed just overshadow and effects of increased contact area.

As Bob Jewett indicated, the amount of friction is for the most part independent of the size of the contact area. You can get a feeling for why this is true by considering that the compression force acting perpendicular to the surfaces functions as sort of pressure, even though we're dealing with solid objects. The force is distributed over the area of contact. For a given amount of force, a smaller area results in a greater pressure while a larger area results in a smaller pressure. The magnitude of the pressure is in fact the compression force divided by the area, so when you multiply the pressure by the area to get the magnitude of the compression force, not too surprisingly, the area cancels out.

Here is one way of seeing why the friction force diminishes with relative surface speed. It's a complicated subject so this is a blatently amatuerish explanation.

If you picture the surface on the microscopic scale, it consists of tiny mountains and valleys, even on a polished surface. As one surface is moved across the other, the peaks collide. Since the mountains are sloped, the collisions tend to push the surfaces apart as well as resisting the motion, the latter being the friction. The faster the surface motion, the more the surfaces are pushed apart. The mountains now collide at points closer to their summits. Since the mountains are generally more gradualy sloped as you approach their summits (less steep), the direction of the collision force becomes more perpendicular to the surfaces. Consequently, you get less force in the parallel direction. You also get fewer collisions per unit distance of travel because fewer of the mountains of one surface can reach those on the other surface. And, the smaller summit areas are easier to shear off.

All of this leads to less friction.

This may be way too simplistic, perhaps flat out wrong, but it works for me.

Jim