Super cool thank you everyone.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Physics question
- Thread starter RoadHustler
- Start date
Rubber butt cap?
Hi,
Did the cue have a rubber butt cap, or was it the old style (think Hoppe Pro)? If old style, less friction with floor and the cue would begin to slide along horizontally, with increasing horizontal motion as the the cue reached 45 degrees.
Oh, and was the flooring a rug or linoleum?
And if a rubber cap, did it cover the whole bottom, or was there a step to plastic or wood, to give a little bounce before the tip hit?
The real world is never as simple as physics or mechanics.
But you all get partial credit....
Take care,
Nick
Hi,
Did the cue have a rubber butt cap, or was it the old style (think Hoppe Pro)? If old style, less friction with floor and the cue would begin to slide along horizontally, with increasing horizontal motion as the the cue reached 45 degrees.
Oh, and was the flooring a rug or linoleum?
And if a rubber cap, did it cover the whole bottom, or was there a step to plastic or wood, to give a little bounce before the tip hit?
The real world is never as simple as physics or mechanics.
But you all get partial credit....
Take care,
Nick
I want to know who is going to conduct the experiment with their cue to confirm the predicted speed?
:grin:
:grin:
I want to know who is going to conduct the experiment with their cue to confirm the predicted speed?
:grin:
lol. I was going to do it with my iPhone on slow motion video setting, and a background of a graduated scale on a piece of paper, to see how far the stick moves during its last few camera frames of movement, Alas, I just bent my phone, breaking the screen, and now no slow motion camera. lol Bendgate is real.
I redid my analysis to include the rotational kinetic energy that I completly forgot about the first time. I was able to match what Dr Dave did.
Dr Dave, do both the KE(linear) and KE(rotational) have to be about the same point? For example, when the I term in the KE(rotational) goes from the cg of the "rod" to its end, that means that the V term in the KE(linear) is also about that same point, and since it does not translate, it goes to zero? Is that correct?
OR.... can the KE(linear) be about the cg, and the KE(rotational) be about the end?
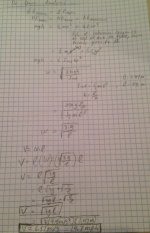
Dr Dave, do both the KE(linear) and KE(rotational) have to be about the same point? For example, when the I term in the KE(rotational) goes from the cg of the "rod" to its end, that means that the V term in the KE(linear) is also about that same point, and since it does not translate, it goes to zero? Is that correct?
OR.... can the KE(linear) be about the cg, and the KE(rotational) be about the end?
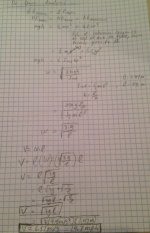
Also, now that I worked out the problem in full by hand, to match what Dr Dave did, I am concerned that the PE uses the h of L/2. If it really should be L/3 (which would represent the typical 58" cue with a 19" balance point), that may make the entire result off by a very significant factor.
PS, I spent hours reading up on rotational KE, and working out this problem! I think I completely skipped that part in school (or more likely skipped those classes to play pool!) Thanks to the OP and to Dr Dave for a motivation back into the schoolbooks
PS, I spent hours reading up on rotational KE, and working out this problem! I think I completely skipped that part in school (or more likely skipped those classes to play pool!) Thanks to the OP and to Dr Dave for a motivation back into the schoolbooks
Last edited:
In my analysis (see below), I show both ways to handle the total kinetic energy (KE). One way is to sum the translational energy of and rotational energy about the CM. The easier way is to use just the rotational energy about the pivot point (which accounts for both effects via the parallel axis theorem).I redid my analysis to include the rotational kinetic energy that I completly forgot about the first time. I was able to match what Dr Dave did.
Dr Dave, do both the KE(linear) and KE(rotational) have to be about the same point? For example, when the I term in the KE(rotational) goes from the cg of the "rod" to its end, that means that the V term in the KE(linear) is also about that same point, and since it does not translate, it goes to zero? Is that correct?
OR.... can the KE(linear) be about the cg, and the KE(rotational) be about the end?
BTW, the first equation I derived for v_tip (before making the long, thin cylinder approximation) applies to any cue of any length, weight, balance point, and mass moment of inertia.
Regards,
Dave
I tested this out in real life last night using the stop watch on my cell phone and my Szamboti. Just kidding.  I performed the test 5 times with the cue taking between 1-4-1.5 seconds to hit the floor from a vertical position. Individual results may vary, but I think this is close enough for this discussion.
I performed the test 5 times with the cue taking between 1-4-1.5 seconds to hit the floor from a vertical position. Individual results may vary, but I think this is close enough for this discussion.
Based on that data, using a 58" cue, the average velocity would be V = arc length/t = (pi*r/2)/t = (3.1416*58"/2)/1.4 sec = 65.1 in/sec or 5.4 ft/sec or 3.7 mph.
Kelly
Based on that data, using a 58" cue, the average velocity would be V = arc length/t = (pi*r/2)/t = (3.1416*58"/2)/1.4 sec = 65.1 in/sec or 5.4 ft/sec or 3.7 mph.
Kelly
Last edited:
I tested this out in real life last night using the stop watch on my cell phone and my Szamboti. Just kidding.I performed the test 5 times with the cue taking between 1-4-1.5 seconds to hit the floor from a vertical position. Individual results may vary, but I think this is close enough for this discussion.
Based on that data, using a 58" cue, the velocity would be V = arc length/t = (pi*r/2)/t = (3.1416*58"/2)/1.4 sec = 65.1 in/sec or 5.4 ft/sec or 3.7 mph.
Kelly
That looks like the average speed of the tip, over the 90 degree arc. Of course it is not traveling at a constant velocity, but rather, it is accelerating the entire time. So the maximum velocity of the tip would be at the instant just before the cue impacts the floor.
Fun thread.
Last edited:
Correct, that is average velocity.
That looks like the average speed of the tip, over the 90 degree arc. Of course it is not traveling at a constant velocity, but rather, it is accelerating the entire time. So the maximum velocity of the tip would be at the instant just before the cue impacts the floor.
Fun thread.
One way to test it in real life is with one of the new smartphones that does slow motion video at 120 frames per seconds.
Set up the camera on the floor, and make a background of a ruler printed on a piece of paper. Drop the stick in front of the paper.
Review the footage, one frame at a time, one or two frames before it hits the ground. You will see how far the stick moved between the last few frames. Then you will have the instantaneous velocity for the last 1/120th or 2/120th of a second.
Set up the camera on the floor, and make a background of a ruler printed on a piece of paper. Drop the stick in front of the paper.
Review the footage, one frame at a time, one or two frames before it hits the ground. You will see how far the stick moved between the last few frames. Then you will have the instantaneous velocity for the last 1/120th or 2/120th of a second.