Colenso Deflection Theory Part 2
Colenso Theory of Deflection: Part 2 Grip and Deflection
In part one of this series we learned about the current understanding of cue ball deflection and were introduced to a criticism of this generally accepted theory. In part 2 I will talk about the role that grip plays in deflection.
A diagram was presented at the end of part 1, to show that off center contact with the cue ball will produce no deflection if that contact has complete grip or a perfectly parallel transference of momentum. But as we do experience deflection on off center hits in the real world, I propose that in fact, we should not accept the idea that there is perfect grip, or no slip at the contact point. In fact, these terms are inappropriate to use to describe what is going on during a collision.
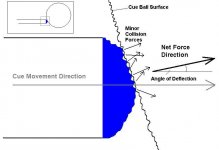
In reality, millions of minor elastic collisions are occurring at the surface interface. The attached diagram illustrates this idea.
By looking at the Tip to Cue Ball collision this way, it becomes obvious, that the main determinants of deflection are the surface characteristics of the two objects. Evidence of this is easily observed in the following situations:
1. Balls colliding deflect at almost 90 degrees.
2. Tips without chalk deflect at high angles. (Without obvious feeling of a miscue).
3. Poor quality chalks or tips deflect more.
4. Quality tips well chalked deflect less.
This evidence is observational, and hasn’t been tested in detail, but to most players they will seem quite obvious.
So why do tests show that tip endmass and distance from center are the key factors in determining cue ball deflection? The answer to this is quite simple. During testing, the tip and chalk qualities are kept almost constant.
With these new insights of the Colenso Theory of Deflection, a whole new horizon of experimental design becomes possible. This theory puts into perspective the most significant developments of cue technology in history. These were the invention of the leather tip by Francois Mingaud and the invention of what was then called twisting chalk by John Carr in the early 1800’s. Both of these developments reduced deflection of off center shots by large amounts as well as increasing the capacity to put spin on the cue ball.
We are now forced to re-examine the 2 factors that have been presumed as the only determinants of cue ball deflection.
Off Center Hit Deflection Factor: Obviously, the further off center we strike the cue ball, the greater will be the amount of minor collisions in a direction away from the line of the cue.
Tip Endmass Deflection Factor: This is harder to ascertain with any precision or certainty, but I will propose the following reason. While many of the contact points are supported along a line of connected molecules running up the length of the cue, a percentage of these contact points apply force across the line of the cue. The resultant forces for these contact points will be increased by a higher weight endmass. This theory suggests that the key in reducing tip endmass deflection will be to reduce the density at the very near end of the cue. Primarily at the tip and the end of the ferrule. Beyond one inch from the cue tip, additional weight will have a negligible effect.
With these new insights, we must consider a new range of factors that influence cue ball deflection. These include, but are not limited to chalk, tip, ferrule, ball and shaft properties. Part 3 in this series will investigate these factors and the influence they could have on future cue designs.
End of Part 2
Colenso Theory of Deflection: Part 2 Grip and Deflection
In part one of this series we learned about the current understanding of cue ball deflection and were introduced to a criticism of this generally accepted theory. In part 2 I will talk about the role that grip plays in deflection.
A diagram was presented at the end of part 1, to show that off center contact with the cue ball will produce no deflection if that contact has complete grip or a perfectly parallel transference of momentum. But as we do experience deflection on off center hits in the real world, I propose that in fact, we should not accept the idea that there is perfect grip, or no slip at the contact point. In fact, these terms are inappropriate to use to describe what is going on during a collision.
In reality, millions of minor elastic collisions are occurring at the surface interface. The attached diagram illustrates this idea.
By looking at the Tip to Cue Ball collision this way, it becomes obvious, that the main determinants of deflection are the surface characteristics of the two objects. Evidence of this is easily observed in the following situations:
1. Balls colliding deflect at almost 90 degrees.
2. Tips without chalk deflect at high angles. (Without obvious feeling of a miscue).
3. Poor quality chalks or tips deflect more.
4. Quality tips well chalked deflect less.
This evidence is observational, and hasn’t been tested in detail, but to most players they will seem quite obvious.
So why do tests show that tip endmass and distance from center are the key factors in determining cue ball deflection? The answer to this is quite simple. During testing, the tip and chalk qualities are kept almost constant.
With these new insights of the Colenso Theory of Deflection, a whole new horizon of experimental design becomes possible. This theory puts into perspective the most significant developments of cue technology in history. These were the invention of the leather tip by Francois Mingaud and the invention of what was then called twisting chalk by John Carr in the early 1800’s. Both of these developments reduced deflection of off center shots by large amounts as well as increasing the capacity to put spin on the cue ball.
We are now forced to re-examine the 2 factors that have been presumed as the only determinants of cue ball deflection.
Off Center Hit Deflection Factor: Obviously, the further off center we strike the cue ball, the greater will be the amount of minor collisions in a direction away from the line of the cue.
Tip Endmass Deflection Factor: This is harder to ascertain with any precision or certainty, but I will propose the following reason. While many of the contact points are supported along a line of connected molecules running up the length of the cue, a percentage of these contact points apply force across the line of the cue. The resultant forces for these contact points will be increased by a higher weight endmass. This theory suggests that the key in reducing tip endmass deflection will be to reduce the density at the very near end of the cue. Primarily at the tip and the end of the ferrule. Beyond one inch from the cue tip, additional weight will have a negligible effect.
With these new insights, we must consider a new range of factors that influence cue ball deflection. These include, but are not limited to chalk, tip, ferrule, ball and shaft properties. Part 3 in this series will investigate these factors and the influence they could have on future cue designs.
End of Part 2