I've read and heard some ignorant comments over the last 3 years concerning the "complicated" math with Poolology. Here's a video showing how the system was created, or at least showing the mathematical theorem that lead to the creation of the system.
A combination of math and physical experimentation was used to design and analyze system numbers, but when it comes to using the system there is no complicated math to perform, unless dividing double digit numbers in half is considered "complicated" for you.
Anyway, for those interested in how a simple mathematical approach was used to create a more advanced fractional aiming system, here it is....
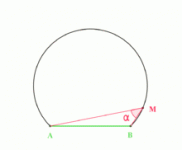
Poolology and the Inscribed Angle Theorem
A combination of math and physical experimentation was used to design and analyze system numbers, but when it comes to using the system there is no complicated math to perform, unless dividing double digit numbers in half is considered "complicated" for you.
Anyway, for those interested in how a simple mathematical approach was used to create a more advanced fractional aiming system, here it is....
Poolology and the Inscribed Angle Theorem
![CropperCapture[92].jpg CropperCapture[92].jpg](https://forums.azbilliards.com/data/attachments/413/413948-2653b3b87e72c90831551ea93d4bed51.jpg?hash=JlOzuH5yyQ)