I like to check out the statistics of various things (even though stats often don't tell the whole story).
Jay and CJ were discussing whether the Mosconi Cup's format
(multiple short races) is a good test that would even out luck enough for the best team to win.
And there's also been discussion of TAR's shorter races to 20-something vs. a single race to 100.
I'm an amateur at this stuff so anyone with better math, tell me if this is wrong.
I use this handy calculator which is sort of like a coin flip calculator, but you can "weight" the flip.
http://stattrek.com/online-calculator/binomial.aspx
So, we're interested in the odds that a worse player can still come out on top based on the race format.
Let's say the worse player is only 2% worse... in 100 games, he should win 48.
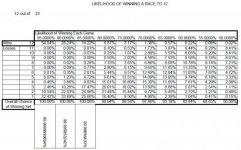
Odds that the worse player will win in single race to 5: ~45%
Odds that the worse player will win in a long race to 100: ~28.6%
So, race to 100 more fair than race to 5, duh.
But, what if we had a series of races to 5?
The Mosconi cup is race to 11 SETS, meaning whoever wins 11 races-to-5.
Well, we already figured out the worse player might still prevail 45% of the time, in a single race to 5.
What are the odds that will happen 11 (or more) times, out of 21 sets?
The math says 32.4%.
If you were to convert the mosconi cup into games, and every match went hill-hill, we're talking
a maximum of 9 games per set, out of 21 sets. That's 189 games.
So if the mosconi cup were a single long race, it would be race to 95 (just over half of 189 games).
What are the odds the same underdog can win in a race to 95?
The math says 29%.
The short version:
Racing to 5 gives a slight (2%) underdog about a 16% edge vs. racing to 100.
Not as big as I would have thought.
With only a 2% difference in skill, the underdog can still win over 1/4th of the time in a race to 100.
You'd need an absurdly long race to be 'pretty sure' the best player wins. You'd need to go to like 1,000
before the better player is ~90% to win the whole set, with such a small difference in skill.
21 races to 5 (Mosconi Cup format) gives the underdog about a 3.4% edge over a single long race.
Also not as big as I thought. Obviously the actual mosconi cup will have lots more complexity.
Some guys will be 2% underdogs, others will be 10%, and the underdogs are spread between both teams.
But the point is, a series of short races isn't much different from a single long race.
Applying this logic to TAR:
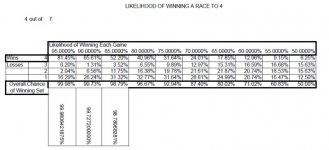
Single race to 100, we already know a 2% dog still has a 28.6% chance to win.
What if it's 3 races to 30? (the upcoming tar is 2 races to 30 and then a shorter race in 1p).
The math says the underdog wins each race ~37.9%.
So the odds of winning 2 out of 3 of these: ~32.2%
Best of 3 sets [race to 30] gives a slight (2%) underdog about a 3.6% edge vs. racing to 100.
So, is the mosconi cup a fair test of skill? I'd say it's pretty close to fair, if you think race to 100 as fair.
But even a race to 100 still allows a slight underdog to win between 1/4th and 1/3rd of the time.
I should mention the numbers change pretty drastically if you make the difference in skill go from
"slight" (2%) to not-quite-as-slight (5%).
The 2% dog wins 28.6% of his races to 100.
The 5% dog wins 7.8% of his races to 100.
The 2% dog gets a 3.4% edge by breaking up all the mosconi matches into races to 5.
The 5% dog gets closer to a 5% edge.
The 2% dog gets 3.6% edge switching up a race to 100 into 3 races to 30.
The 5% dog gets a nice 8.7% boost from this format.
So, the bigger the gap in skill, the more helpful it is to break long races up into multiple shorter ones.
Jay and CJ were discussing whether the Mosconi Cup's format
(multiple short races) is a good test that would even out luck enough for the best team to win.
And there's also been discussion of TAR's shorter races to 20-something vs. a single race to 100.
I'm an amateur at this stuff so anyone with better math, tell me if this is wrong.
I use this handy calculator which is sort of like a coin flip calculator, but you can "weight" the flip.
http://stattrek.com/online-calculator/binomial.aspx
So, we're interested in the odds that a worse player can still come out on top based on the race format.
Let's say the worse player is only 2% worse... in 100 games, he should win 48.
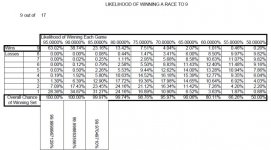
Odds that the worse player will win in single race to 5: ~45%
Odds that the worse player will win in a long race to 100: ~28.6%
So, race to 100 more fair than race to 5, duh.
But, what if we had a series of races to 5?
The Mosconi cup is race to 11 SETS, meaning whoever wins 11 races-to-5.
Well, we already figured out the worse player might still prevail 45% of the time, in a single race to 5.
What are the odds that will happen 11 (or more) times, out of 21 sets?
The math says 32.4%.
If you were to convert the mosconi cup into games, and every match went hill-hill, we're talking
a maximum of 9 games per set, out of 21 sets. That's 189 games.
So if the mosconi cup were a single long race, it would be race to 95 (just over half of 189 games).
What are the odds the same underdog can win in a race to 95?
The math says 29%.
The short version:
Racing to 5 gives a slight (2%) underdog about a 16% edge vs. racing to 100.
Not as big as I would have thought.
With only a 2% difference in skill, the underdog can still win over 1/4th of the time in a race to 100.
You'd need an absurdly long race to be 'pretty sure' the best player wins. You'd need to go to like 1,000
before the better player is ~90% to win the whole set, with such a small difference in skill.
21 races to 5 (Mosconi Cup format) gives the underdog about a 3.4% edge over a single long race.
Also not as big as I thought. Obviously the actual mosconi cup will have lots more complexity.
Some guys will be 2% underdogs, others will be 10%, and the underdogs are spread between both teams.
But the point is, a series of short races isn't much different from a single long race.
Applying this logic to TAR:
Single race to 100, we already know a 2% dog still has a 28.6% chance to win.
What if it's 3 races to 30? (the upcoming tar is 2 races to 30 and then a shorter race in 1p).
The math says the underdog wins each race ~37.9%.
So the odds of winning 2 out of 3 of these: ~32.2%
Best of 3 sets [race to 30] gives a slight (2%) underdog about a 3.6% edge vs. racing to 100.
So, is the mosconi cup a fair test of skill? I'd say it's pretty close to fair, if you think race to 100 as fair.
But even a race to 100 still allows a slight underdog to win between 1/4th and 1/3rd of the time.
I should mention the numbers change pretty drastically if you make the difference in skill go from
"slight" (2%) to not-quite-as-slight (5%).
The 2% dog wins 28.6% of his races to 100.
The 5% dog wins 7.8% of his races to 100.
The 2% dog gets a 3.4% edge by breaking up all the mosconi matches into races to 5.
The 5% dog gets closer to a 5% edge.
The 2% dog gets 3.6% edge switching up a race to 100 into 3 races to 30.
The 5% dog gets a nice 8.7% boost from this format.
So, the bigger the gap in skill, the more helpful it is to break long races up into multiple shorter ones.