The thinner the cut the greater the precision needed to make shots - for any kind of aiming.
pj
chgo
Last edited:
Fractional aiming and required accuracy
- Thread starter Bob Jewett
- Start date
pj
chgo
I'm referring specifically to aiming. The further out the more oblique and low res those fractions become. I think CP avoids the curvature trap entirely by establishing the cue ball direction.
For those who are technically inclined, the error allowed is proportional to the cosine of the cut angle. The cosine is 1.0 for zero cut (full ball) and 0 for 90 degrees on either side. For a 60-degree cut, you have to be twice as accurate (half the margin of error) as for a straight shot.
Another way of saying that is the 60° "effective contact area" on the OB is half the size (from the shooter's perspective) of the straight shot contact area.
Here's a quick chart of the effective OB contact areas (as percentages of the straight shot contact area) for the common fractional CB/OB overlaps:
pj <- any more technically inclined and I'd fall over
chgo
Last edited:
I try always measure/guess cut angle and effects(spin, throw, deflection etc) before i shoot and chart tells me where to aim. It takes away a lot of visual tricks what balls do. So i am actually just aiming cueball to certain line with desired english and speed. What i guess before shot. Then every cut is the same. Accuracy needed is to make the shot different as you can see from previous posts but this way i can simplify aiming process and get more consistent play overall.
Really? Doesn't this same fat out "oblique and low res" view apply to the contact point also? Actually even more so. The curvature of ob is always a trap with contact points from a distance. With fractional aiming there is no curvature trap -- the ob is viewed as a 2D circle with a fixed/consistent diameter for every shot.
Since you're comparing, contact points simply line up. It's far more practical to fine tune point to point than an approximate fraction. For instance if you aim and shoot everything point to point instead of whatever you aim fractionally, eventually you will have an EXACT reference for everything you shoot however thick or thin. I can't see fractions or any other method doing that.
You can certainly get as precise estimating fractions as you can estimating contact points - probably more so since they're always in the same places on the OB. More importantly, fractions are references from which the precise final aim is estimated.
pj
chgo
Prolly but you cannot get moar preciserer den geosynchronous aleining. The math thing with all the shapes.
probably 3-4 years since i checked contact point. CJ said it somewhere so nicely. "One can´t find point from round object(ball). it will move around"
I agree that 100%
Since i stopped looking it my game instantly got more solid. bad days not so bad that used to be.
CJ’s problem with contact points isn’t everybody’s - I (and many others) can easily visualize them and use them successfully.
To each his/her own.
pj
chgo
That would be true if u can always pick contact points perfectly. It is quite hard to thing to do IMO. I tried to do it years and finally gave up.
I just want to clarify also little bit. I just wanted to give shout out to this fractional aiming thread because it is close what i am using. I think it is complicated stuff to teach and especially learn. So many beginner/low level players don´t often see or feel it good. And after they learn other ways to aim they don´t be comfortable to start using it and i think that is shame. I hoped i would pick this right from start. That´s said it is not suitable for everyone anyways. Some people just dont have that kind of head to think mathematics to fully benefit from this kind of aim.
But again... it need of mathematics can be bypassed by learning a ton of reference shots.
But again... it need of mathematics can be bypassed by learning a ton of reference shots.
There are usually reference marks on the ball but regardless you use contact points to line up the shot and not necessarily to aim it. There are many ways to see the exact hit. Jimmy Reid's EAO (equal angle opposites - his term) for instance. I make this work by dropping a vertical line to the cloth and pivoting from that clearly visible tangent through that line, to the reciprocal tangent on top of the cue ball. This tiny 3/8" line segment provides very accurate socketing information. Other ways include bisecting the object ball along the pocket line. Draw a vertical line through the exit point and shoot away the far slice with the reciprocal slice on the cue ball. There's the mid point roll which PJ diagrammed a while back. You can match the carom tangents. Make a right angle with your thumb and index finger. Line the index along the edge of the object ball pointing to the pocket. The thumb goes perpendicular across the ass of the ball and shows the carom exit. ABSOLUTELY NONE of these alignments require knowing the contact point on the front of the cue ball though you can easily take a peek at it just to make sure it's there lol... It's all eye training from there; no tricks, just the shot, the whole shot, and nothing but the shot.
Ok. Maybe, but I don´t really want to know anymore details of other systems. I did achieve century break player level on snooker and keep winning of Finnish Kaisa tourneys(which is super accurate potting game while getting caroms for bonuses on 11 ft tables(67mm ball 70mm pocket), not mention to pool. AFTER i changed my aiming to this kind fractional aiming. I just aim with my stick. not ball overlap. I also line use carom angles to give my brain more information about shots. I also play pretty ok Russian pyramid which is carom cueball in super tight 12 ft tables so i some knowledge about it too. Like how speed and sidespin AFFECT carom angle. Thats a lot.
As i said i don´t care how others do it but wanted to give shout out to this topic i saw.
Very good. Expanding my view, (and I wish there were kaisa type pockets available in the states) snooker breaks, rotation stacks and even the sacred 14.1 require mastery of certain pet patterns - licks if you will, just to keep from screwing up. True accomplishment would delimit all that pedantia and it starts with hitting the shot perfectly.Ok. Maybe, but I don´t really want to know anymore details of other systems. I did achieve century break player level on snooker and keep winning of Finnish Kaisa tourneys(which is super accurate potting game while getting caroms for bonuses on 11 ft tables(67mm ball 70mm pocket), not mention to pool. AFTER i changed my aiming to this kind fractional aiming. I just aim with my stick. not ball overlap. I also line use carom angles to give my brain more information about shots. I also play pretty ok Russian pyramid which is carom cueball in super tight 12 ft tables so i some knowledge about it too. Like how speed and sidespin AFFECT carom angle. Thats a lot.
As i said i don´t care how others do it but wanted to give shout out to this topic i saw.
One aiming method is to imagine the 2-D overlap of the cue ball as it lands on the object ball and connect the amount of overlap to the cut angle. The common fractions and their approximate degrees of cut are:
full ball -- 0 degrees -- straight shot
3/4 full -- 15 degrees
1/2 full -- 30 degrees
1/4 full -- 45 degrees
1/8 full -- 60 degrees
Except for the half-ball hit which is 1/2 full and a cut of 30 degrees, those numbers are all slightly off, but the errors are not important for this first part of the discussion. Another factor that must eventually be considered is throw which varies with the speed and spin of the cue ball but that gets very complicated and it is better to completely understand the simple fundamental ideas of the situation before we get into all the nasty details. Those details are important and we'll get to them.
View attachment 574666
In the diagram you see a shot off the spot and five different areas where the five fractional aims will be useful. Let's consider the straight shot or 0 degree cut. How wide is that area? The pocket is two balls wide (more or less) and the two extreme arrival positions of the object ball are shown by the 2 ball and the 3 ball. If you draw straight lines from the centers of those balls back to the 1 ball, you get the angular width of the pocket. It is about 4 degrees. If the object ball is sent more than 2 degrees away from dead center of the pocket, it won't go in. (Again, this is not perfectly accurate. From this approach angle, the pocket is larger for very hard shots, so the pocket size varies with the shot conditions. Pick your own number if you don't like 4 degrees of pocket width.)
Where can the cue ball be in order to pocket a straight shot to that pocket off the spot? It is pretty obviously the red shaded area marked "0°". If the cue ball is anywhere on the bottom/right side of the shaded area, with a perfect, full hit the object ball will pass over the position of the 2 ball. If the cue ball starts on the top/left side of the shaded area the cue ball will pass over the position of the 3 ball. If the cue ball is anywhere outside the red shaded area, a full hit won't pocket the object ball.
The same argument applies to the other standard fractional cuts. It is not hard to see that all the triangular areas for the different cuts are 4 degrees wide. This means that the standard fractional cuts for a shot as hard as a spot shot cover only about 1/4 of the area of the table. The "good" triangles are 4 degrees wide and 15 degrees apart.
But it is a really, really bad idea to wed yourself to exact fractional ball hits. Just consider the straight shot. If the cue ball is on one edge of the red shaded area, and you use a true fractional aim, you will send the 1 ball all the way to the extreme side of the pocket. If your stroke makes a small error in that same direction, you will miss the shot. Since most of us make small errors most of the time (and large errors the rest of the time), you will end up missing about half of such shots.
The lesson from this is that the "good" triangular areas for the shot are actually considerably smaller. If you are willing to give up half of the allowed error to your aiming system, then the triangles will shrink to 2 degrees wide and the percent of the table that is covered by these fractional aims drops by a factor of two to roughly 1/8th or 12.5% of the table surface.
Excellent post, Bob! FYI, I've quoted it on the limited lines of aim resource page, where related analyses can be found. This page is also linked from the fractional-ball aiming resource page.
Good work,
Dave
FYI, here's a useful template from the how to estimate and visualize a cut angle resource page, which includes ball overlaps, contact points, and cut angles corresponding to minute markers of a clock face, for a wide range of ball-hit fractions:
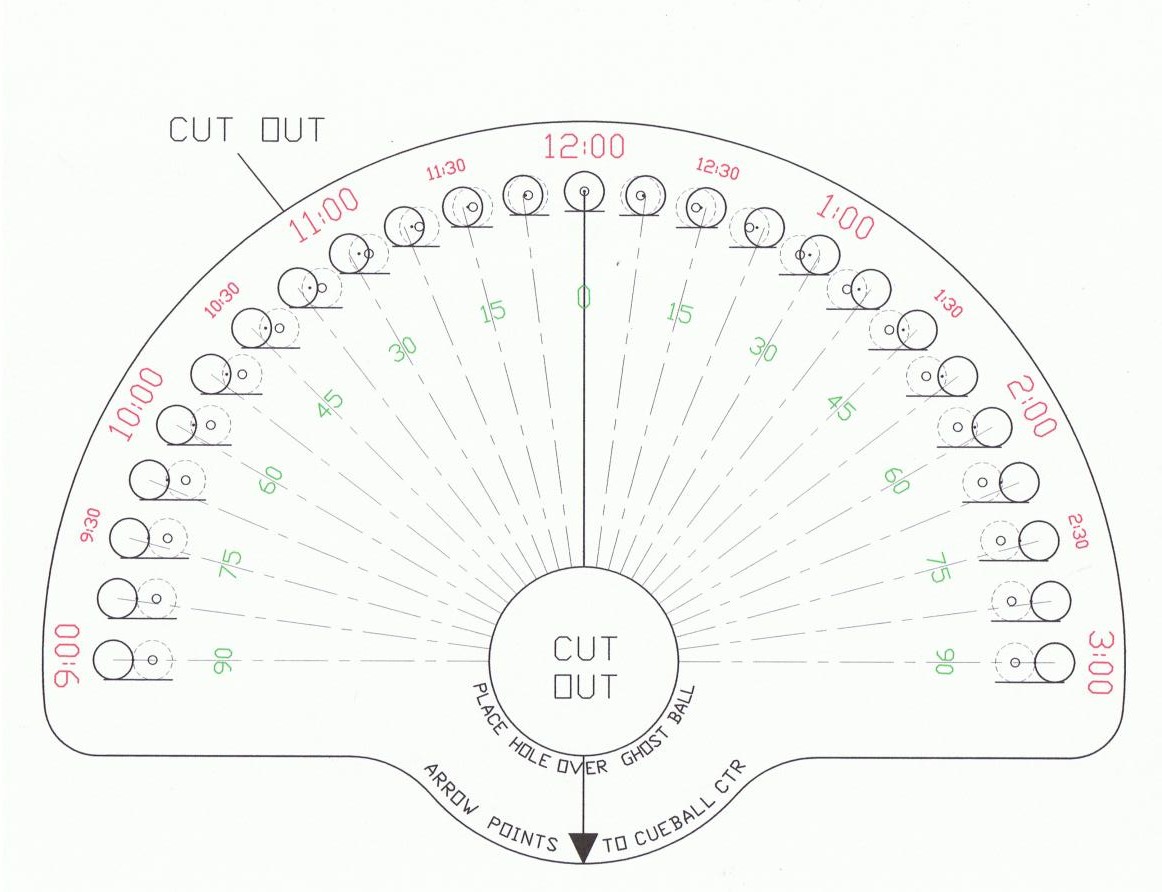
One aiming method is to imagine the 2-D overlap of the cue ball as it lands on the object ball and connect the amount of overlap to the cut angle. The common fractions and their approximate degrees of cut are:
full ball -- 0 degrees -- straight shot
3/4 full -- 15 degrees
1/2 full -- 30 degrees
1/4 full -- 45 degrees
1/8 full -- 60 degrees
Except for the half-ball hit which is 1/2 full and a cut of 30 degrees, those numbers are all slightly off, but the errors are not important for this first part of the discussion. Another factor that must eventually be considered is throw which varies with the speed and spin of the cue ball but that gets very complicated and it is better to completely understand the simple fundamental ideas of the situation before we get into all the nasty details. Those details are important and we'll get to them.
View attachment 574666
In the diagram you see a shot off the spot and five different areas where the five fractional aims will be useful. Let's consider the straight shot or 0 degree cut. How wide is that area? The pocket is two balls wide (more or less) and the two extreme arrival positions of the object ball are shown by the 2 ball and the 3 ball. If you draw straight lines from the centers of those balls back to the 1 ball, you get the angular width of the pocket. It is about 4 degrees. If the object ball is sent more than 2 degrees away from dead center of the pocket, it won't go in. (Again, this is not perfectly accurate. From this approach angle, the pocket is larger for very hard shots, so the pocket size varies with the shot conditions. Pick your own number if you don't like 4 degrees of pocket width.)
Where can the cue ball be in order to pocket a straight shot to that pocket off the spot? It is pretty obviously the red shaded area marked "0°". If the cue ball is anywhere on the bottom/right side of the shaded area, with a perfect, full hit the object ball will pass over the position of the 2 ball. If the cue ball starts on the top/left side of the shaded area the cue ball will pass over the position of the 3 ball. If the cue ball is anywhere outside the red shaded area, a full hit won't pocket the object ball.
The same argument applies to the other standard fractional cuts. It is not hard to see that all the triangular areas for the different cuts are 4 degrees wide. This means that the standard fractional cuts for a shot as hard as a spot shot cover only about 1/4 of the area of the table. The "good" triangles are 4 degrees wide and 15 degrees apart.
But it is a really, really bad idea to wed yourself to exact fractional ball hits. Just consider the straight shot. If the cue ball is on one edge of the red shaded area, and you use a true fractional aim, you will send the 1 ball all the way to the extreme side of the pocket. If your stroke makes a small error in that same direction, you will miss the shot. Since most of us make small errors most of the time (and large errors the rest of the time
The lesson from this is that the "good" triangular areas for the shot are actually considerably smaller. If you are willing to give up half of the allowed error to your aiming system, then the triangles will shrink to 2 degrees wide and the percent of the table that is covered by these fractional aims drops by a factor of two to roughly 1/8th or 12.5% of the table surface.
I started playing in 1960 (at 13 in a smoky pool hall) without an aiming system or taking into consideration fractions, cosines, tangents and sines which all were taught in a classroom and not in a pool room. Call it instinct or great hand/ eye coordination or maybe mindlessness but I beat a lot of good players in pool rooms and roadhouses in East Texas. I had no idea that squirt or throw or the speed of the cloth and the cleanliness of the balls played a part in shooting. Since then I’ve read about and experimented with every “aiming system” only to return to visualization. I visualize the rotation (spin) of the cue ball and it’s affect on the rotation of the object ball as it heads towards my target. I would never start off a young pool player and with any of the theories that I have read about or experimented with for fear of making them too mechanical. This is coming from someone that has taken advanced math and physics courses in college. You have to have some feel for the game or your going to find yourself in a trap.