how many 2.25 pool balls fit on a 9 ft 50 x 100 billiard table?

[OTLB]

I will submit this to my legal department of Dewey, Cheetem, and Howe.

my counsel has summoned me to chambers at the local poolroom for consultation. I am thinking I never said the balls were perfect, just that they were 2.25 pool balls. On one hand math doesn't lie, but the real question of how many fit? given inconsistency in ball diamater etc I am not really sure 1098 pools would fit.

The variance between the balls avg diameter and the other numbers given must be considered. How accurate would the balls have to be to fit 1098?

This is key to knowing whether they would.

 

[scruffy1]

First, Way to go sidepocketmike! Very entertaining! I do not believe you guys had firmed up the bet though! Sorry!


Brains numbers were verfied by me as I did it with actual balls before I started the thread.OTLB "quote"

What happened????

 

[brain]

Given more than 1000 balls, I think the variation in diameters would all even out and that you'd be able to fit at least 1098. There is a chance that more could fit if the standard deviation and distribution was just right.

There may still be another solution that could be more than 1098 using combinatorics. I thought this may have been what SidePocketMike was going to use - I'm actually a little disappointed that it was so simple (and I missed it!). If I find the time to write the algorithm - or get a friend to do it for me - I'll post if its greater than 1098.

Combinatorics output ends up looking something like this (I can't believe this thread went here!):

 

[OTLB]

First, Way to go sidepocketmike! Very entertaining! I do not believe you guys had firmed up the bet though! Sorry!


Brains numbers were verfied by me as I did it with actual balls before I started the thread.OTLB "quote"

What happened??

Like I said. I used real balls

 

[Cuephoric]

New heads of the Accounting Department for AZb Mechanics!

Mike, welcome to the forums- you're hired.
Alongside of Brain, I believe you two can correctly calculate the odds of what numbers hitting for me in the next lotto, thus enabling me to not only win the lottery, but also know what numbers to pick for the raffles on AZ!
You two get a percentage of course....

 

[OTLB]

what is the spec on a pool ball?

is it.005?

 

[Majic]

what is the spec on a pool ball?

is it.005?

http://www.wpa-pool.com/index.asp?content=rules_spec

The WPA tolerance on balls is +.005 and table size is +.125 both directions

 

[OTLB]

The 1098 Ball Proof

Place 22 balls evenly spaced along the 50" rail so that the end balls are both in the corner of the table (touching both rails).
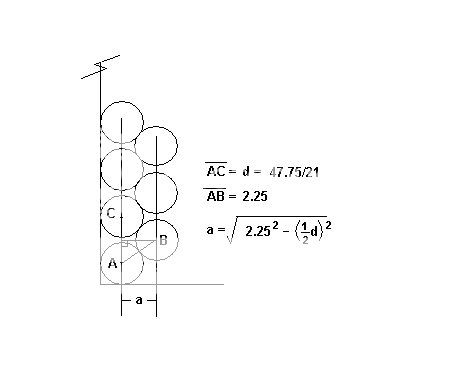
The distance between balls centers should be d = 47.75/21 =~2.2738095238095238095238095238095 inches

Place the 21 balls in the next row so each ball is in contact with 2 of the balls in row 1.

Let the distance between the parallel rows of balls be called a...
and a = sqrt( 2.25^2 - .5 * d) =~1.9416352804680586159754603442379 inches

Place 49 rows of balls in this manner, alternating 22, 21, 22, 21, etc.

49 rows of balls = 25x22 + 24x21 = 1054 balls

The rectangular space taken up by these balls is the full 50" width of the table by length L
L = 48a + 2.25 =~95.44849346246681356682209652342 inches

What is significant here is that there is now ~4.55" x 50" of felt left. More than enough to arrange 2 additional rows containing 22 balls each or 44 more balls for a grand total of 1098.

The spreading of the rows to use all 50" of the table allows the distance a here to be a tiny bit smaller than in Brains example where the balls are tight.
His value for a = 2.25 x sin 60 = 1.9485571585149869552183771341941

The difference per row is less than 7 thousands of an inch, but it gets you one more ball on the table.

I patiently await my $100.



Added pic: Gaps between balls exaggerated for clarity

Ok real question again, how many pool balls will fit? Your first step is to evenly space 22 balls within an accuracy of 30 decimal points between each other.

Who can do that?

 

[OTLB]

Ok real question again, how many pool balls will fit? Your first step is to evenly space 22 balls within an accuracy of 30 decimal points between each other.

Who can do that?

As soon as you touch one the other will move

 

[brain]

Ok real question again, how many pool balls will fit? Your first step is to evenly space 22 balls within an accuracy of 30 decimal points between each other.

Who can do that?

Seriously, there is plenty of room for 1098. If you put 1098 balls on the table they will settle into place - its not necessary to accurately place each one. It should be just as easy to put 1098 on the table as 1097. For 1097, its like racking them all tight; for 1098 the outer balls of the 22 rows touch the side rails and the 21 ball rows are racked tight into the gaps, so its only necessary to make sure the balls are tight (the same as is necessary for 1097).

 

[Club Billiards]

Ok real question again, how many pool balls will fit? Your first step is to evenly space 22 balls within an accuracy of 30 decimal points between each other.

Who can do that?

I'd bet that I could reasonably evenly space the first row of balls enough to touch both side rails. Nevermind nevermind...before this bet gets out of hand, it seems to me that if you place the first row, then the second, you could push the second rown into the first to space them out.

 

[SidePocketMike]

Ok real question again, how many pool balls will fit? Your first step is to evenly space 22 balls within an accuracy of 30 decimal points between each other.

Who can do that?

In practice, jiggleing a board across the first few rows should help the balls settle into an approximate position... As long as the balls are allowed to utilize the entire 50", there should be no problem fitting them in. Actually, tossing an additional ball on top of the last two rows and vibrating the table may cause enough of a shift in the balls to allow 1099!

Did someone say they tried this with 1097 balls? Did you think of taking a photo?

 

[brain]

SidePocketMike's 1098 solution

Here's an illustration of SidePocketMike's 1098 solution. The math is in his post (very cleaver, by the way).

I agree that more might be possible; I have submitted the problem to someone I know and hope that he will have time to run the problem on his computer.

 

[emf123]

Nice job, SidePocketMike!!!!

Brain - way to man up, nice illustration!!!

OTLB - time to admit defeat (as if )

 

[SidePocketMike]

Here's an illustration of SidePocketMike's 1098 solution. The math is in his post (very cleaver, by the way).

I agree that more might be possible; I have submitted the problem to someone I know and hope that he will have time to run the problem on his computer.

Nice image! Origanally I thought that by offsetting the sets of two balls in the two final rows might gain enough space for 2 more balls. But hand calculations were never completed... After 4 rows I gave up as it didn't look like space was trending up fast enough. If your not following me, this was my thought...

Put the top left two balls tight against the end cushion and put the next two tight against the "rack"... Alternating like this gets you more space as the rows get closer to the middle, as they can be placed farther into the "rack" as the spaces line up... Do 11 rows from the top and do the same with the bottom 11 starting from the bottom cushion. I don't think you can fit 2 more in, but 1 will probably go if you can manipulate the 1054 rack of balls minutely.

 

[OTLB]

Nice job, SidePocketMike!!!!

Brain - way to man up, nice illustration!!!

OTLB - time to admit defeat (as if )

Well, OTLB quote#3 show me a good looser and I will show you a looser and of course then theres You can't win them all

Regardless, it was a fun thread!

 

[brain]

SidePocketMike's 1099 solution!

Nice image! Origanally I thought that by offsetting the sets of two balls in the two final rows might gain enough space for 2 more balls. But hand calculations were never completed... After 4 rows I gave up as it didn't look like space was trending up fast enough. If your not following me, this was my thought...

Put the top left two balls tight against the end cushion and put the next two tight against the "rack"... Alternating like this gets you more space as the rows get closer to the middle, as they can be placed farther into the "rack" as the spaces line up... Do 11 rows from the top and do the same with the bottom 11 starting from the bottom cushion. I don't think you can fit 2 more in, but 1 will probably go if you can manipulate the 1054 rack of balls minutely.

So that everyone can follow:

Although it actually fits in my illustration, I didn't use a CAD program and by the looks of it there's too big of a gap between the last row and the end rail. So I doubt that it will actually fit; but I may work through the calculation at some point - I'll wait for the combinatorics solution first.

 

[SidePocketMike]

So that everyone can follow:

Although it actually fits in my illustration, I didn't use a CAD program and by the looks of it there's too big of a gap between the last row and the end rail. So I doubt that it will actually fit; but I may work through the calculation at some point - I'll wait for the combinatorics solution first.

As drawn you got 1101 in there... Way to go, but... Your last two rows have 23 balls each!!!?!

The illustration seems a little off since we should only have 5/100 of an inch left after the two rows of 22!

But that is exactly what I was trying to do!!

 

[OTLB]

keep going and RKC might be right

 

[n10spool]

no no no RKC cant be right again I hate when he does that it scares me...lol