If you were surprised by this and some of your other results, then you haven't been studying your Coriolis!

This and much more was derived almost 200 years ago in his masterwork of billiard physics,
Théorie mathématique des effets du jeu de billard published in 1835. Luckily for you guys, there's an
English translation by David Nadler available now. (I slogged my way through the original French years ago with a dictionary and grammar reference and my brain is still aching.)
This stuff was also revisted by Régis Petit in
Billard : Théorie du jeu, which is really just a chapter-by-chapter restatement of most of Coriolis' results in more modern notation.
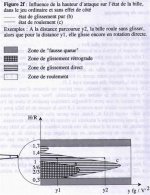
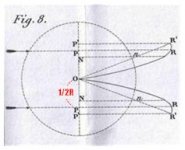
I've attached an image of figures 8-10 from Coriolis for reference:
- Figure 8 shows spin vs tip offset and how max rpms aren't at max offset.
- Figure 9 shows ball speed vs tip height, and how it peaks around %20 above center.
- Figure 10 is a composite of 3 graphs of distance vs tip height. The first (I's) shows distance to the sliding/stun state (peak around %30 below center); the second (Q's) shows distance to natural roll (peak around %10 below center); and the third (K's) are just the distance to parabola vertices used in his constructions in figures 6-7.
For comparison, I also attached Petit's version of figure 10 which is a little easier to read out of context.
Robert