... and apparently a training ball
Sharivari on aiming....
- Thread starter Bob Jewett
- Start date
I don't know if any of the houligans can even make sense of these latest service packs
The Emperor hasn't had any clothes for a long time. Why be honest now?
They did argue manual pivot to the center of the cue ball on a dead straight shot or spot shot was the bomb.
Yeah, that’s about where I tuned out
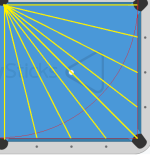
This system seems to say that for two angles a and b, tan(a-b) = tan(a)-tan(b). That has a significant error especially for larger angles. If you are going to use numbers in a system it's better to use the correct numbers.
The example you show will be close because one of the lines is nearly parallel to a rail.
A good way to study the accuracy of this system is to take a bunch of positions within the system and find the angle from the system and compare it to the actual angle with an accuracy of 0.1 degree.
(The 0.1 is to ensure that you don't get lazy on the arithmetic. It's not required for most shots. )
their manual pivots were proven to be gimmicks so they went to " disguised " pivots
Oikawa
Well-known member
Hmm, not sure if I'm following what you mean. I don't see how tangent function is related to it. My explanation was probably poorly written and hard to follow, but the basic idea is that you measure the potting angle in degrees by using table geometry/diamonds as a measuring device. This obviously doesn't account for throw etc, just a way of measuring the cut angle in degrees neatly. To make it practical, you can convert that angle value into a ball overlap value to aim at.
The rise in a given length (four diamonds) is proportional to the tangent of the angle (relative to the bottom rail in your picture).
The formula you show in effect claims that tangents are equal (proportional) to angles. That is false. This is fairly simple geometry/trig.
Oikawa
Well-known member
I see, I get it now. Good to know, didn't realize this before.
I guess the simplest fix to decrease the margin of error (not completely, but by a good amount), would be to memorize the general trend or precisely how much the error is at each angle and just add/subtract that much from the measurements along the way.
Without precise numbers, the trend to fix the error would be that, the closer to 45 degrees (4 diamonds) you are, the more you'd shift the measurement away from the 45 degree side.
4 diamonds -> no adjustment
3 diamonds -> move 0.3 diamonds
2 diamonds -> move 0.2 diamonds
1 diamond -> move 0.1 diamonds
For anything else, you can interpolate.
I guess the simplest fix to decrease the margin of error (not completely, but by a good amount), would be to memorize the general trend or precisely how much the error is at each angle and just add/subtract that much from the measurements along the way.
Without precise numbers, the trend to fix the error would be that, the closer to 45 degrees (4 diamonds) you are, the more you'd shift the measurement away from the 45 degree side.
4 diamonds -> no adjustment
3 diamonds -> move 0.3 diamonds
2 diamonds -> move 0.2 diamonds
1 diamond -> move 0.1 diamonds
For anything else, you can interpolate.
Attachments
Last edited:
Seems a bit complicated, a lot of guesstimation, doesn't it?
With Poolology, the OB is at 26. The cb-ob centerline lands at about 13 or 14 on the end rail (not quite 1.5 diamonds from the pocket. Immediately this tells me a halfball aim will pocket the ball. No guesswork.
I think this method shares some of Poolology's simplification ethic - projecting the OB and CB paths onto the half table centerline allows easy memorization of fractional aim benchmarks on that line for visual comparison with actual cut angles.
pj
chgo
boogieman
It don't mean a thing if it ain't got that ping.
Unfortunately, he now of course accuses me of being childish behavior or whatever and all I have asked him to do is do exactly what he claimed he could do extremely easily do."I can make a simple CAD drawing to explain it!"
...
...
...
He said he can easily prove CTE with CAD. I said that works be great, that would settle the debate once and for all.
Now he always has a reason/excuse why he will not do what he claimed he can easily do.
Just seems so strange too behave like that.
I've learned you just have to let these things go eventually. He stepped in it, maybe didn't really understand what he was saying or the audience he was saying it to and isn't man enough to own up. It goes into the database that creates a reputation, good, bad or mixed.
There have been two DVD's.
30+ some videos . Not counting the dozens of other variations.
A 6 lbs book.
Still no diagram.
The best one is by Dr Dave.
And they haven't made.their own to counter Dr Dave's.
Also bear mind using Poolology’s system, since it’s based on the OB being within 4ft-8” of the CB, the longer you are away from the OB, especially on 9ft tables, you have to compensate by aiming a tad thicker!
Sort of correct, but not quite...
It's true that with fractional aiming (when keeping the cb and ob on the same line anyway), one has to aim thinner as the cb gets closer to the ob. However, after a distance of about 2ft between the balls, the angle difference is so small that it really isn't much of an issue.
Example: Setup a halfball shot with 3ft between cb and ob. Lets say the halfball aim pockets the ball dead-center pocket. If you move the cb another 3ft back along the same centerline between the balls, making it a 6ft distance now, the same halfball aim will result in the ob being overcut by less than 1°. That's typically not enough to warrant any aiming adjustment or compensation.
With Poolology, the system is most accurate within a certain cb-ob distance (about to 2 to 5 feet). This is because that's the parameters used to design the system. Beyond 5ft isn't much of an issue, but as the distance gets closer than 2ft, especially nearing 1ft, the shots will begin to come off too thick to hit the pocket.
It's an interesting thing, and it's more prevalent on thinner cuts than thicker cuts. A 3/4 aimed shot (about a 15° cut angle) has a difference of only 0.8° when comparing a 2ft cb-ob distance to a 5ft distance. The same aim at a 1ft distance will come off 2.1° thicker when compared to the 5ft distance.
A difference of 0.8° is no problem, but 2° can definitely cause a miss.
A halfball aim has a difference of 1.6° when comparing a 2ft shot to a 5ft shot. But the difference between a 1ft shot distance and a 5ft distance is 4.3°. That's a big miss!
So aiming thinner than the system indicates is a definite must as the cb gets closer to the ob, but very seldom is aiming thicker at longer distances required.