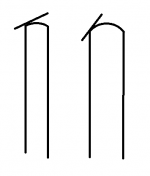So, I have been contemplating how to post this for a week, and still can't quite wrap my head around how to explain this without confusing everyone, but I will give it my best shot.
Often when discussing tips, the first question is "what radius do you like, dime or nickel"... well while this is easy to gauge, and if all shaft diameters are the same, is a fair assesment of what you may like.
However, the idea of a set radius ONLY works on a given shaft size, and here is why.
I have several shafts in my arsenal... my main shaft is 13.3mm, and I have 3 more 12.7, 12.2, 11.7, 11.5
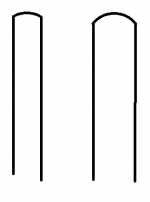
What I discovered is, that every shaft that I have, has a DIFFERENT radius on it. The reason for this, is that a given radius (lets use nickel for arguments sake) have different curvatures on different size tips.
On a 13.3mm shaft a nickel radius has a fairly steep curve and will allow a high degree of spin to be applied to the cue ball, but conversely a nickel radius on a 11.75mm shaft is pretty darn flat, and disallows a high degree of spin to be applied.
A better way of "thinking about tip radii" is the the about the tangent vector that the curve departs the edge of the tip. What this means is, if you think about the angle that the tip ends where the curve meets the edge of the tip, you will get a much more consistent curvature if you have different size tips, on several shafts.
I had several diagrams drawn up to help explain this, but am at work and cannot attach the photos. I hope this makes sense to you all, and maybe someone else good jump in and give their opinion (and if you understand, help with the illustration)
Often when discussing tips, the first question is "what radius do you like, dime or nickel"... well while this is easy to gauge, and if all shaft diameters are the same, is a fair assesment of what you may like.
However, the idea of a set radius ONLY works on a given shaft size, and here is why.
I have several shafts in my arsenal... my main shaft is 13.3mm, and I have 3 more 12.7, 12.2, 11.7, 11.5
What I discovered is, that every shaft that I have, has a DIFFERENT radius on it. The reason for this, is that a given radius (lets use nickel for arguments sake) have different curvatures on different size tips.
On a 13.3mm shaft a nickel radius has a fairly steep curve and will allow a high degree of spin to be applied to the cue ball, but conversely a nickel radius on a 11.75mm shaft is pretty darn flat, and disallows a high degree of spin to be applied.
A better way of "thinking about tip radii" is the the about the tangent vector that the curve departs the edge of the tip. What this means is, if you think about the angle that the tip ends where the curve meets the edge of the tip, you will get a much more consistent curvature if you have different size tips, on several shafts.
I had several diagrams drawn up to help explain this, but am at work and cannot attach the photos. I hope this makes sense to you all, and maybe someone else good jump in and give their opinion (and if you understand, help with the illustration)