Hi Jal, how ya been? Been a while since we've last had a discussion.
I've been okay and good to see you posting every once in a while. Ah, for the good old days! Please forgive my long delay in responding, but I wanted to take a fresh look at the problem given the issues you raise below. I based my statement on the results of a program of several years ago where, as I recall, the CB speed changes seemed to correlate with the changes in the sine of the ghostball angle. However, I believe I must have been looking at using inside english to increase the cut angle and increase CB speed down the tangent line, rather than outside to slow it down. There are some cases where there is a somewhat strong correlation (at least, that's my story!).
I agree there is a modest reduction in CB's post-impact speed, and that it can be significant enough when the balls are close together, but it's not clear to me that the greater reduction in ghost ball angle has anything to do with it (other than it being a byproduct of the balls being closer together). I think all that matters is the amount of throw the CB exerts on the OB, and that the maximum amount of throw possible generally increases as the balls are closer together.
Well, I think you're essentially right, though I believe the reduction in ghostball angle has something to do with it. But it alone does not provide an accurate characterization of the speed reduction, contrary to what I confidently exclaimed earlier! Here's a graph showing the fractional reduction in speed down the tangent line as compared to the "predicted curve" (red) using only the sines of the ghostball angles.
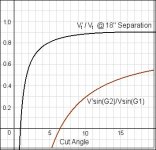
Not good! In fact the change in ghostball angle grossly overestimates the reduction (at least in this case where we're assuming 5 degrees of throw).
But given the two cases where the CB is 6" and 18", assuming that the CB contacts the OB at the exact same trajectory angle, with the same exact same spin, and with the exact same velocity, then the CB would end up in exactly the same place in both cases, regardless of where the CB started, correct? But for the 6" case, the reduction in ghost ball angle is greater. So is the reduction in ghost ball angle actually relevant?
I'm sorry jsp, I'm just not grasping your argument, perhaps because of my general confusion concerning the whole issue. One thing I am sure of, I was wrong and I thank you for challenging my assumptions.
Since we're on the subject (or were almost a week ago ), here are some plots at different separations between the centers of the CB and OB. All are for stun shots. They indicate the CB's speed reduction down the tangent line when using outside english to "reverse throw" the OB by 5 degrees, as compared to using no english with normal throw. With the outside english, the geometric cut angle as well as the CB's speed are reduced so that the OB's velocity (speed and direction) is identical to the no english case. This makes for a fair comparison.
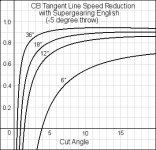
As the graphs indicate, the reduction is very significant, even at the larger separations, for very small cut angles. (Of course, you're reducing something very small to begin with, but reducing it a lot, nevertheless.

) Where the curves drop down into negative territory, both the CB and OB would be traveling on the same side of their original line of centers (Bob Jewett's challenge).
Since travel distance is proportional to the square of a ball's speed, squaring the fractional speed gives you the fractional travel distance.
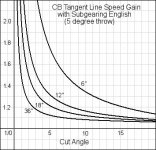
The opposite effect, boosting CB tangent line speed, is shown below. Here, inside or "subgearing" english is employed to increase the geometric cut angle. The OB's velocity is again identical for the no english and inside english cases.
Jim


